Mai fidarsi della bellezza - Inganni e illusioni di un criterio scientifico
La bellezza può essere una splendida guida per lo sviluppo di formalismi matematici, ci suggerisce in questo blog Matteo Donolato (Che bella equazione! – Il ruolo della bellezza nelle scienze) seguendo il pensiero di P. Dirac.
Ai fisici teorici, in particolare, piace maneggiare teorie e oggetti matematici “belli”, addirittura considerano l’eleganza come un criterio di successo delle formulazioni teoriche, delle spiegazioni della realtà, delle descrizioni dei sistemi fisici.
Tuttavia sembra necessario essere cauti, perché a volte la bellezza matematica può nascondere dei tranelli.
Un bel formalismo matematico, infatti, ha il pregio di rendere la descrizione della realtà più semplice, più maneggevole, apparentemente più efficace e più elegante, ma, spesso, non rappresenta la realtà nel suo modo di essere effettivo, nei suoi comportamenti fenomenici.
Proviamo a fare qualche esempio:
- Il primo può essere l’identità di Eulero: è bellissima, compatta e semplice; comprende una serie di elementi che ricorrono in tutte le matematiche e geometrie – euclidee e non – ma, poiché è un’identità, non significa altro che un oggetto è identico a sé stesso, seppur descritto in modi diversi.
Esattamente come Hesperus e Vesperus, la stella del mattino e la stella della sera; nomi diversi per la stessa cosa, vista da angolazioni diverse, ma pur sempre una e una sola cosa è: il pianeta Venere.
L’identità di Eulero racconta di come la bellezza matematica possa diventare un formalismo di nessuna utilità nella pratica scientifica e applicativa.
È opportuno ricordare Husserl[1], quando accusava Galileo e, con lui, molta scienza della modernità, di realismo metafisico, di aver dimenticato – inseguendo i formalismi idealizzati – il contatto con il mondo delle cose reali.
Un secondo esempio – dobbiamo però per un attimo dimenticare che è stato falsificato nel ‘600 – è il modello geocentrico aristotelico-tolemaico dell’universo con la terra, con noi/io al centro di tutto. Cosa c’è di più bello, simmetrico, elegante, appagante, soprattutto per chi lo ha disegnato, di questo modello? Secondo il punto di vista antico era anche efficace nella rappresentazione della realtà. In parte anche per il nostro punto di vista: nella nostra esperienza quotidiana, non pare anche a noi di essere fermi, con il cielo che ci gira intorno?
Come sappiamo, però, questo schema non ha retto il confronto con i paradigmi successivi; per cui, è “caduto” ed è stato sostituito da un altrettanto elegante modello (quello di Newton) basato su un formalismo matematico, anch’esso, come ci dice Matteo Donolato, di grande bellezza: la legge della gravitazione universale.
Ecco, quindi, il terzo esempio: la legge di gravitazione universale si basa su un “oggetto scientifico”[2] misterioso e mai dimostrato: la forza di attrazione gravitazionale, cioè un’azione a distanza tra due corpi macroscopici.
“Oggetto” che è stato a sua volta sostituito, nella teoria della relatività, dalla nozione di campo gravitazionale. Che fa a meno della forza.
Il quarto ed ultimo esempio di bellezza teorica e matematica, nel campo della fisica delle particelle, è la Teoria supersimmetrica delle stringhe (o supersimmetria); questa teoria è in grado – grazie a dei formalismi matematici giudicati molto eleganti da quasi tutti i fisici – di descrivere il mondo dei bosoni e dei fermioni, e converge nella Teoria del Tutto: un tentativo di unificazione delle teorie quantistica e relativistica.
La “supersimmetria” – teoricamente – permetterebbe anche di aver a che fare con quantità e numeri vicine all’unità, che molti fisici definiscono “naturali”; e di evitare di far uso del cosiddetto “fine tuning”, cioè di aggiustamenti della teoria – assimilabili alle cinture di protezione di Lakatos – a fronte di casi particolari e risultati non allineati con le previsioni.
La teoria della supersimmetria, però, non sembra dare frutti sperimentali. Nessuno dei suoi risultati riesce a essere testato, con ovvio fastidio dei fisici che hanno puntato sulla sua produttività potenziale.
----------------
Al contrario, possiamo fare degli esempi di formalismi “non così belli” che – almeno per ora – sono di successo e (abbastanza) testati sperimentalmente.
Il modello che descrive una cosa apparentemente banale come i pennacchi di fumo (avete presente quelli che escono dalle ciminiere?) è costituito da un sistema di equazioni che - già in una approssimazione semplificata - riempiono almeno due pagine di un normale libro di testo – solo come formalismo matematico.
Purtroppo, un pennacchio di fumo non può essere descritto con formule prese dalla geometria solida; è, invece, un oggetto di grandissima complessità in cui compaiono più di un centinaio di fattori e termini e ancora non ne è descritta completamente la struttura. È più brutta di un orco delle favole. Ma funziona piuttosto bene.
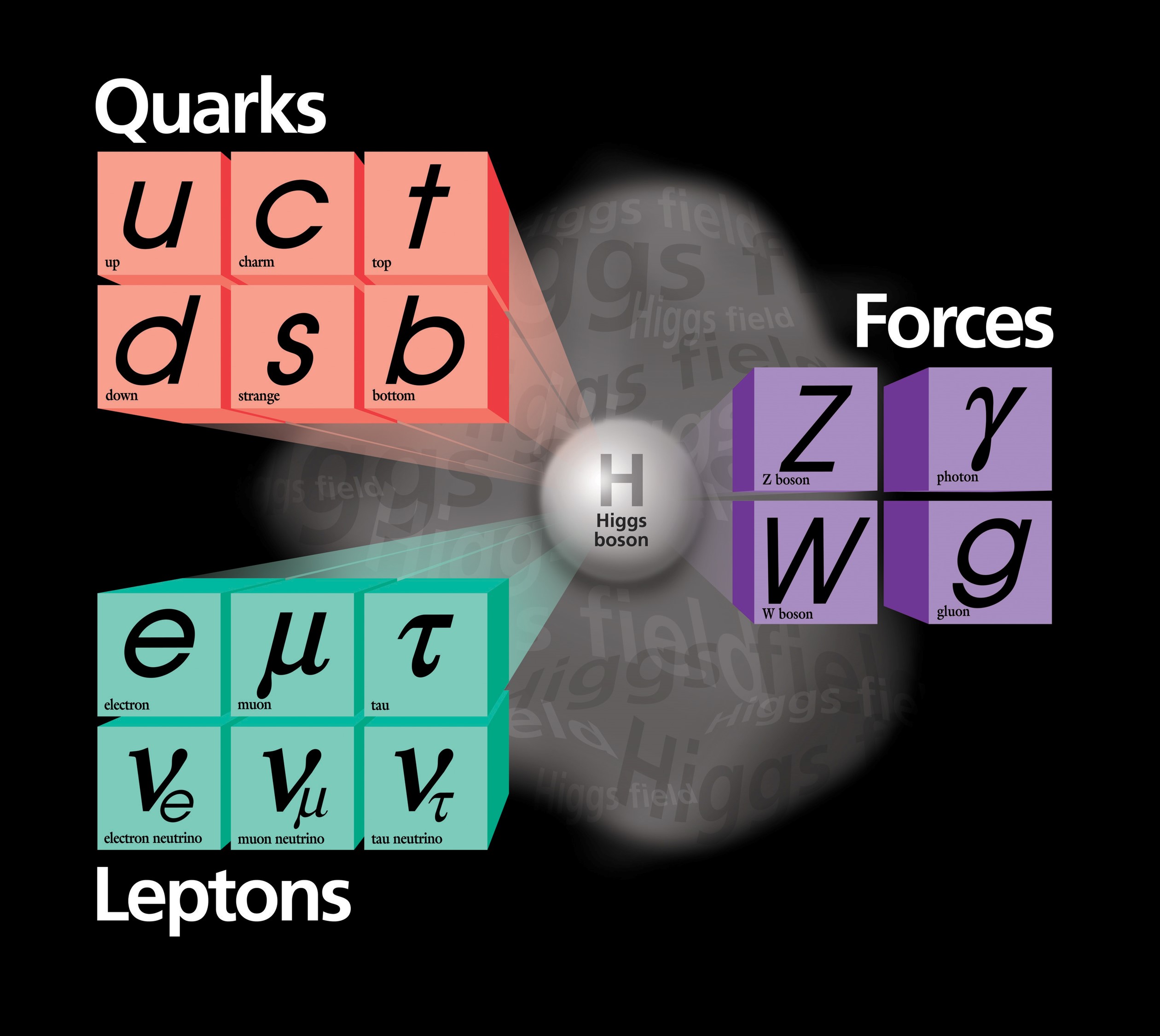
In fisica delle particelle, il "Modello standard", teoria che resiste da alcuni anni e che ha numerosi riscontri sperimentali – non ultima la rilevazione del bosone di Higgs, previsto anni prima e ora “trovato” e misurato sul campo – è abbastanza orribile, se misurata con il criterio della bellezza e dell’eleganza: più di 25 particelle “elementari”, tra cui: 6 fermioni detti quark; 8 gluoni privi di massa; 6 leptoni, che non partecipano alle interazioni forti; il fotone; 3 bosoni massivi; in ultimo il bosone di Higgs, massivo, neutro elettricamente e funzionale a dare massa a fermioni e bosoni. Tutti questi suddivisi in tre generazioni, in funzione della massa; inoltre, le generazioni non sono definite da criteri matematici a priori ma solo dalla necessità di “far funzionare” il modello (se mi si passa la semplificazione). “Vi delude che il modello standard sia così brutto?” dice Sabine Hossenfelder[3]
--------------
Sembra, quindi, estremamente pericoloso per i fisici, per i naturalisti - e direi persino per gli economisti - che desiderano descrivere in maniera realistica l’universo, affidarsi a dei formalismi molto belli.
Pericoloso perché il mondo e l’universo, nel loro presentarsi sono per lo più disuniformi, presentano continuamente singolarità, sfuggono al principio di omogeneità.
I casi eleganti come, ad esempio, le strutture polimorfe oggi chiamate frattali, sono eccezioni notevoli; tanto che uno strutturalista nato nella matematica come Roger Caillois, li presenta e li esalta proprio come eccezionalità, come fenomeni notevoli.
I salti, le catastrofi, le singolarità, sono la norma della realtà.
In fisica e nelle scienze naturali è meglio non fidarsi - e non affidarsi - alla bellezza matematica.
Si rischia di perdere la strada…
NOTE
[1] E. Husserl, La crisi delle scienze europee e la fenomenologia trascendentale, Il Saggiatore, Milano, 2015
[2] L. Daston, Biographies of scientific objects, The University of Chicago Press, Chicago and London, 2000
[3] S. Hossenfelder, Sedotti dalla matematica, Raffaello Cortina Editore, Milano, 2019, pag. 182
Distopia tecnoscientifica e immaginazione - Il mondo nuovo di A. Huxley
Non sono un romanziere - soleva dire Huxley - ma un saggista che scrive fiabe.
Perché, allora, affidare alla forma del romanzo una previsione sul futuro?
Per quale ragione proprio la «superorganizzazione» dell’ardito mondo nuovo e dei suoi fantasmagorici prodotti tecnoscientifici, frutto della più fervida capacità immaginativa, sembrano annunciare l’estinzione di quest’ultima?
Perché, infine, il mondo d’Utopia gravita sopra di noi con fare minacciosamente distopico?
- Utopia, distopia e tecnica
«Il secolo delle macchine comincia a farsi sentire»[1]. Sono le parole dell’architetto Charles-èdouard Jeanneret-Gris, in arte Le Corbusier (1887-1965). Sempre lui, nel medesimo volume Urbanistica (1925), scriveva con il suo solito ottimismo quasi messianico che «crollava soltanto un mondo vecchio. Su dalle rovine stava arditamente spuntando un mondo nuovo»[2].
È questo lo spirito che anima certe frange avanguardistiche dei primi decenni del secolo scorso, come quando un giovane Antonio Sant’Elia (1888-1916) dichiarava che «come gli antichi trassero l’ispirazione dell’arte dagli elementi della natura, noi - materialmente e spiritualmente artificiali - dobbiamo trovare quell’ispirazione negli elementi del nuovissimo mondo meccanico»[3].
Ancora, è il medesimo mondo che anni più tardi il filosofo Gunther Anders (1902-1992) avrebbe dipinto con tinte fosche e apocalittiche nel
suo L’uomo è antiquato I (1956): «mondo della «matrice»[4] e del «dislivello prometeico»[5], asincronia della psiche umana rimasta irrimediabilmente indietro rispetto alla lineare, efficiente e funzionale perfezione dei «suoi» prodotti tecnoscientifici. Una psiche debole e imperfetta che arranca dietro alla perfezione macchinica, e che modella il suo «umiliante ideale»[6] sulla fredda perfezione che contraddistingue la macchina, «il suo sogno, va da sé, sarebbe quello di diventare uguale alla sua divinità: agli apparecchi, o meglio, di essere compartecipe - in certo modo consustanziale - della loro natura»[7].
-----------
Qualche decennio prima, sempre nella prima metà del secolo scorso, apparve per la prima volta nelle librerie Brave New World (1932) dell’autore inglese Aldous Huxley (1894-1963), racconto fiabesco di una società ideale in cui domina una superorganizzazione di natura tecnoscientifica secondo i tre canoni della «Comunità, Identità e Stabilità»[8]. Utopia o distopia?
Di distopie non si è sempre parlato.
La parola stessa, a essere generosi, non ha più di duecento anni. Ma quand’anche facessimo della distopia l’immagine in negativo dell’utopia, ci accorgeremmo, forse con imbarazzo, che neppure di quest’ultima abbiamo una definizione tanto chiara.
È Thomas More a costruire il neologismo e ad affidarlo al suo omonimo racconto del 1516[9].
A seconda dell’etimo l’utopia è un «non-luogo» (U-topia) o un «buon-luogo» (Eu-topia).
Tuttavia, il «non» dell’utopia nulla ha a che spartire con la recente caratterizzazione dell’antropologo Marc Augé (1935-2023)[10]: il «non» di un’utopia definisce il «luogo» come ciò che non è ma dovrebbe essere, «città ideale», come quella descritta dal frate domenicano Tommaso Campanella (1568-1639) ne La città del sole (1623).
----------
Huxley aveva a cuore queste distinzioni, tutt’altro che quisquilie o eruditismo da scaffale: egli scrisse una «distopia», Il mondo nuovo, e una «topia»[11], l’isola (1962), ma non si intrattenne mai con l’utopia.
Perché ciò è determinante?
Il «non» dell’utopia, si è detto, non ha alcunché di negativo: è come la storia della tensione amorosa in Platone, immagine a cui tendere.
Perciò, propriamente parlando, l’etimo è una fusione piuttosto che un’alternativa: «non luogo» che, correlativamente, è un «buon luogo».
Si potrà forse obbiettare che un tale racconto è, nonostante tutto, frutto di una mente o di un cervello, che «l’idealità» dell’utopia è frutto della «dannata immaginazione» che ci lega a terra.
Tuttavia, More e Campanella fanno dell’immaginazione un veicolo di purificazione, l’immagine «ideale» dev’essere intimamente legata a una simbologia teologica, garante di un’intima e sacra connessione con il cosmo, «cosmo in piccolo».
In Brave New World nulla di tutto ciò: non è l’immagine della città in armonia con il cosmo, ma piuttosto lo schema di un’ingegnosa macchinazione, di uno schema-mondo, «comunità che grazie all’identità realizza la stabilità»[12].
Non è soltanto l’inversione dell’utopia. Nella narrazione distopica c’è una riformazione della «funzione immaginativa».
Non si tratta più di un veicolo verso l’idealità, ma di un’estensione immaginativa della scienza stessa.
L’immaginazione estende il prodotto tecnoscientifico nelle sue possibilità d’insieme, all’estremo.
Anders da ciò impara il fondamentale principio metodologico dell’«esagerazione», per cui il «dislivello» dell’uomo rispetto ai suoi prodotti richiede, per essere capace di controbattere, una metodologia altrettanto esagerata; insomma «esistono fenomeni che non si possono trattare senza accentuarli e ingrandirli»[13].
L’esagerazione consiste allora nell’estrema immaginazione del prodotto tecnoscientifico: la nascente eugenetica diviene catena di montaggio per esseri umani a base di «ipnopedia» e «persuasione chimica», la nascente farmacologia diviene il soma, «la droga perfetta…euforica, narcotica, gradevolmente allucinante…tutti i vantaggi del Cristianesimo e dell’alcol; nessuno dei difetti»[14].
Ogni prodotto è sviluppato, attraverso l’immaginazione, nella sua singola possibilità utopica: droga senza effetti collaterali, eugenetica senza errori - o quasi -, vita senza tristezza, coraggioso mondo nuovo scevro dal peso del passato; anche la casa, «psichicamente squallida» e fonte degli «attriti della vita che vi si ammucchiavano»[15], è stata scongiurata.
Eppure, di distopia si tratta, e quest’ultima vive un gemellaggio singolare con lo sviluppo tecnoscientifico: che si possa «estendere il presente» è il vago principio comune che li anima.
- Immaginazione
Se l’immaginazione tecnoscientifica è indeterminata nel campo del futuro (ragion per cui si «cerca di immaginare cosa accadrà in questo o quel caso»), se l’indeterminatezza è, per così dire, il «campo base» dell’immaginazione, allora Huxley giunge a un esito volutamente paradossale: l’immaginazione approda al tempo futuro della sua estinzione, laddove nulla può essere indeterminato, là, nella «tirannia del benessere di Utopia»[16].
È il tratto più profondo del Mondo nuovo: se il silenzio è potenziale fonte d’indeterminazione[17], allora è necessario sostituirlo con la musica continua e sensuale dei «sessofonisti», con gli spettacoli ipnotici del «cinema odoroso»; se il processo ontogenetico fatto di genitori «vivipari» è fonte d’imprevedibilità, allora bisognerà sostituirlo con un processo di produzione umana che non lasci spazio al dubbio. Osserviamo un altro elemento, altrettanto profondo.
Se uno dei personaggi principali, tale Bernard Marx, è capace di guardare con una dose di sospetto il mondo in cui vive, ciò è dettato dal suo essere «errore» della catena di montaggio: «dicono che qualcuno si sia sbagliato quando era ancora nel flacone»[18].
Possiamo spingerci ancora più in là: nel mondo di Huxley è in atto una sistematica eliminazione del passato, nutrita dalle stesse ragioni di fondo. La «riserva dei selvaggi del New Mexico» dove esseri umani imperfetti e retrogradi «conservano le loro abitudini e i loro costumi ripugnanti»[19] è uno spazio esterno a Utopia.
La riserva sta al di là della città dell’efficienza, percepita da chi vive nel mondo nuovo con un misto di disgusto e timore.
La memoria storica è esternalizzata e rigettata, racchiusa nella riserva che dista diversi giorni di viaggio - non ci sono vecchi nella città ideale. Diversamente, i ricordi custoditi nella città dei civilizzati è pura «memoria operativa», «memoria che ripete senza immaginare», una «memoria priva di passato»[20]; la storia - ripetono i bambini «in training» - «è tutta una sciocchezza»[21].
La vuota memoria fa tutt’uno con l’esclusione dell’imprevedibilità, «la macchina gira e rigira, e deve continuare a girare, sempre. È la morte che si ferma»[22].
Nel mondo nuovo, prendendo in prestito le parole di un saggio apparso di recente, si può dire che «si è liberi di scegliere tutto quello che c’è in menù»[23].
Insomma, tra utopia e distopia avviene una sorta di ritorcimento temporale: il «non luogo» dell’utopia come immagine ideale e principio morale è scivolato nel «non luogo» della distopia come timore che, effettivamente, questa possa realizzarsi.
Perciò, in esergo, Huxley riporta un passo del filosofo Nikolaj Berdjaev (1874-1948), «le utopie appaiono oggi assai più realizzabili di quanto non si credesse un tempo. E noi ci troviamo attualmente davanti a una questione ben più angosciosa: come evitare la loro realizzazione definitiva?»[24]
Se l’utopia è una freccia rivolta verso un futuro ideale, la distopia tecnoscientifica è il tentativo di figurarsi ciò che potrebbe avverarsi già domani, incubo imminente, o come osservava Huxley nella prefazione del 1946, «oggi sembra quasi possibile che l’orrore possa ricadere su di noi nell’arco di un secolo»[25].
Insomma, l’espediente narrativo del genere utopico è sempre stato il «distacco onirico»: è necessario risvegliarsi nel mondo nuovo. Nuovamente, c’è una differenza profonda tra utopia e distopia: se nel primo caso il distacco permette, per così dire, di rendere i piedi leggeri e fare del mondo ideale qualcosa a cui elevarsi, nel secondo caso il sogno si fa angoscioso, rischia di filtrare nello stato diurno.
- Complottismo e immaginazione
Ecco alcuni fatti curiosi: se Huxley avesse scritto Brave New World nel secolo nuovo, nulla ci impedirebbe di supporre che, come altri, sarebbe finito nel circondario della categoria fittizia di «complottista».
C’è di più, poiché proprio coloro che finiscono per essere gettati, volenti o nolenti, all’interno di questa «categoria», si adoperano per una costante riappropriazione del racconto distopico tecnoscientifico come modo di reazione al presente - «siamo in 1984!»
Ma, se da una parte chi sente l’invivibilità del presente si rifugia nella razionalizzazione che un racconto può fornire, questa stessa azione di appoggio a un auctoritas alternativa rischia di adombrare la «chiamata originale» del racconto distopico, immaginare.
Giungiamo così a una stazione singolare: la militarizzazione della vuota parola «complottismo», ma potremmo inserirvi anche «negazionismo», punta dritto contro il carattere immaginativo che fa di queste forme narrative un’arma contrapposta frontalmente all’utilizzo politico della tecnoscienza a fini di controllo[26].
Anche la scienza - dice il governatore di Utopia in una tranquilla confessione - deve essere imbavagliata, «la scienza è pericolosa»[27] e ancora, «la nostra scienza è una specie di libro di cucina, con una teoria ortodossa dell’arte della cucina che nessuno ha il diritto di mettere in dubbio»[28].
La «narrazione ufficiale» così precipua in Brave New World - ma vale anche per racconti come 1984 di Orwell, che Huxley elogia profusamente[29] - non solo non sa che farsene dell’immaginazione, deve escluderla sistematicamente. E così, per principio, deve escludere i fuochi d’indeterminazione da cui quest’ultima possa germinare: il silenzio, lo spazio incolto, il discorso svicolato dalla legiferazione; è un «conformismo dinamico», laddove «la riduzione teoretica della molteplicità ingestibile a unità comprensibile si muta in pratica in riduzione della diversità umana a uniformità subumana, della libertà a schiavitù»[30].
Huxley aggiunge: «dobbiamo ritenere più possibile qualcosa che somigli al mondo nuovo e non qualcosa che somigli a 1984»[31]. Infatti, se nel secondo l’immaginazione rimane una possibilità latente di colui che soffre e vuole immaginare qualcosa di diverso - «quando l’individuo sente, la società è in pericolo»[32] -, nel primo la stabilità, alimentata dall’incessante soddisfazione di vuoti piaceri passeggeri, fa dell’immaginazione una scomodità.
-------
Era il 1958 quando Huxley, in conversazione con Mike Wallace, annunciava l’imminente avverarsi delle sue più fantasiose immaginazioni[33].
Sotto la spinta delle forze impersonali della superorganizzazione e della pressione demografica, prolungate a loro volta dal condizionamento «neopavloviano», chimico e subconscio, il mondo nuovo non sembrava più la fantasiosa fiaba di un futuro remoto.
Eppure, non possiamo fermarci a questo: fare di Brave new world la cartina tornasole del reale significa alzare bandiera bianca.
D’altra parte, ridurre le parole di Huxley a finzione significa misconoscerne l’originale chiamata al prolungamento immaginativo che con tanta insistenza, vediamo tutt’ora scoraggiato.
Qual è, quindi, il linguaggio della nostra superorganizzazione?
«Reale», solamente ciò che è stato approvato.
«Possibile e desiderabile», ciò che ne consegue con fredda deducibilità.
«Immaginazione» ciò che vi si adagia sopra come un pacchetto o una copertina,
l’involucro policromo del prodotto perennemente unico.
NOTE
[1] Le Corbusier, Urbanistica (1925), Il Saggiatore, Milano 2017, p. 92.
[2] Ivi, p. 236.
[3] A. Sant’Elia, Architettura futurista, Abscondita, Milano 2022, p. 25.
[4] Si veda G. Anders, L’uomo è antiquato I (1956), Bollati Boringhieri editore, Torino 2003, pp. 97-199.
[5] Ivi, pp. 31-94.
[6] Sulla «vergogna prometeica» si veda Ivi, pp. 40-72.
[7] Ivi, p. 43.
[8] A. Huxley, Il mondo nuovo (1932), Mondadori Editore, Milano 2015, p. 9.
[9] Secondo Françoise Choay è proprio il racconto di More a inaugurare la letteratura utopica. Si veda F. Choay, La regola e il modello (1980), Officina Edizioni, Roma 1986, pp. 181-220.
[10] Per un testo introduttivo si veda M. Augé, Disneyland e altri nonluoghi (1997), Bollati Boringhieri editore, Torino 2009.
[11] Per questa distinzione si veda l’intervista del 1958 tra il poeta John Lehmann (1907-1987) e Huxley, disponibile al seguente indirizzo: https://www.youtube.com/watch?v=pXS5yWatuE8
[12] A. Maurini, “Il mondo nuovo e i suoi ‘ritorni’, in A. Huxley, Il Mondo Nuovo, cit., p. 364.
[13] G. Anders, L’uomo è antiquato I, cit., p. 23.
[14] A. Huxley, Il mondo nuovo, cit., pp. 52-53
[15] Ivi, p. 38.
[16] “Prefazione del 1946” in, A. Huxley, Brave New World, cit., p. 246.
[17] Si veda https://www.controversie.blog/indi-gregory-lopzione-del-silenzio/
[18] A. Huxley, Il mondo nuovo, cit., p. 46.
[19] Ivi, p. 94.
[20] R. Ronchi, Bergson, Christian Marinotti Edizioni, Milano 2011, p. 127.
[21] A. Huxley, Il mondo nuovo, cit., p. 36.
[22] Ivi, p. 42.
[23] B. Castellane, In terra ostile, Signs Publishing, 2023, p. 14.
[24] A. Huxley, Il mondo nuovo, cit., p. 7.
[25] A. Huxley, “Prefazione del 1946” in, Il Mondo Nuovo, cit., p. 246.
[26] Scrive Huxley ne “Ritorno al mondo nuovo”, in Il mondo nuovo, cit., p. 267, «noi vediamo dunque che la tecnologia moderna ha portato alla concentrazione del potere economico e politico, e alla formazione di una società controllata (spietatamente negli stati totalitari, in modo più pulito e nascosto nelle democrazie».
[27] A. Huxley, Il mondo nuovo, cit., p. 202.
[28] Ivi, p. 204.
[29] si veda A. Huxley, “Ritorno al mondo nuovo”, in Il mondo Nuovo, cit., in particolare pp. 265-275.
[30] A. Huxley, “Ritorno al mondo nuovo”, in Il Mondo Nuovo, cit., p. 269.
[31] Ivi, p. 252.
[32] A. Huxley, Il mondo nuovo, cit., p. 87.
[33] Si veda: https://www.youtube.com/watch?v=alasBxZsb40&t=951s
Che bella equazione! – Il ruolo della bellezza nelle scienze
«My work always tried to unite the true with the beautiful;
but when I had to choose one or the other,
I usually chose the beautiful»[1] (H. Weyl)
INTRODUZIONE
L’obiettivo di questo articolo è di riflettere sulla bellezza, una tematica apparentemente semplice e ordinaria ma che si rivelerà, nel corso dell’esposizione, un nucleo problematico da indagare attentamente.
Iniziamo la nostra disamina con una sezione filosofica, per sottolineare che siamo davanti a una questione complessa, che presenta sfumature concettuali profonde e antiche. Successivamente, analizzeremo questo tema da un punto di vista scientifico, con l’intento di mostrare come la bellezza entri a pieno diritto nei discorsi della scienza.
Lo scopo di questo scritto è di decostruire una narrazione ingenua, limitante e simil-scientista, che vede bellezza e scienza come due argomenti lontani e slegati, che non si incontrano mai, come due rette parallele. Mostreremo come tale separazione sia puramente convenzionale, contingente.
1. BELLEZZA E FILOSOFIA
In filosofia, l’analisi della bellezza ha origini antiche; questo tema viene indagato dall’estetica, una disciplina filosofica di ampio respiro che abbraccia numerose tesi e nuclei concettuali come, per esempio, «la produzione e i prodotti dell’arte»[2] o «il giudizio di gusto su di essi»[3].
Platone (427 ca.-347 ca. a.C.) sostiene che la bellezza è collegata all’ordine, alla proporzione e all’armonia; inoltre, la descrive come «la manifestazione più evidente del bene che permea tutte le cose»[4].
Nel Simposio, sviluppa l’idea secondo cui la bellezza attragga Eros (Amore), indicato come un “demone”, un’entità semidivina «sospesa fra cielo e terra»[5]; quindi, «l’amore viene stimolato dalla bellezza, […]: essa è il fine dell’amore, ciò verso cui l’amore riversa il suo slancio»[6].
Nel Fedro, inoltre, Platone afferma che la bellezza sensibile permette all’anima di ricordare l’idea di bellezza, perfetta e divina, ammirata prima dell’incarnazione. Pertanto, la bellezza del mondo fisico, nonostante sia molto lontana dalla compiutezza dell’idea, permette che lo spirito si elevi: «uno, al vedere la bellezza di quaggiù, ricordandosi della vera bellezza mette nuove ali»[7].
Per Platone esistono diverse tipologie di bellezza, ognuna delle quali occupa una posizione gerarchica distinta: sul gradino più basso incontriamo la bellezza del corpo mentre in cima troviamo la bellezza in sé, «idea eterna e immutabile di cui partecipano tutte le cose belle, sia fisiche sia spirituali»[8].
Plotino (205 ca.-270 ca. d.C.), figura centrale del neoplatonismo, «approfondisce e sviluppa la riflessione platonica sul bello, esposta nel Fedro e nel Simposio, associando il bello alla perfezione del mondo ideale»[9]; inoltre, questo autore dedica due trattati alla tematica della bellezza e la sua visione viene a volte qualificata come una “metafisica del bello”[10].
Nel testo enneadico Sul bello, in disaccordo con Platone, Plotino critica l’idea della bellezza considerata nei termini di armonia e proporzione delle parti, specificando che essa si trovi invece in qualità e oggetti semplici, poiché «ogni allontanamento dall’unità verso la molteplicità equivale a una perdita di perfezione»[11].
D’altra parte, Plotino condivide con Platone l’idea che la bellezza abbia valore anagogico, quando afferma che la bellezza sensibile è una tappa del percorso di purificazione dell’anima, cammino che la deve portare sempre più in alto nella scala dell’intelligibile: «compito dell’anima è […] di distogliere gradualmente la propria visione da quei corpi che non sono altro che “immagini e tracce e ombre” della vera fonte della bellezza, e, rientrando in sé, risalire verso quell’Uno […] circondato da ogni parte dal Bello, un “Bello che dispensa la bellezza a tutte le cose […]”»[12].
Pertanto, «è […] attraverso Plotino che si comprende come, nell’Antichità in generale, sia sempre più difficile, e spesso arbitrario, separare il problema della bellezza […] dalle costruzioni metafisiche in cui esso si inserisce»[13].
Infine, neanche per Edmund Burke (1729 ca.-1797) il bello può essere determinato secondo le categorie di armonia e proporzione, perché «l’ordine e la convenienza tra le parti sono […] qualità colte dall’intelletto, là dove l’effetto della bellezza è molto più immediato e sensibile»[14].
Burke contrappone la bellezza a un altro concetto, il sublime: la prima genera l’amore, «una passione […] sociale, intersoggettiva»[15], mentre il secondo dà origine al terrore, un’emozione collegata «alla tendenza di ogni individuo alla propria autopreservazione»[16]. Le divergenze, però, non terminano qui, in quanto il bello «nasce dalla visione di cose piccole e delicate, e dal contatto con tutto ciò che è liscio, levigato, sinuoso»[17]; al contrario, il sublime si origina, per esempio, dalla visione di spazi molto ampi (oceani, montagne ecc.) o dal «sentimento dell’infinito»[18].
2. SEMIR ZEKI E LA NEUROESTETICA: UNO STUDIO
Il neurobiologo Semir Zeki è ritenuto l’iniziatore della neuroestetica, «un filone di ricerca nell’ambito delle neuroscienze che indaga le basi neurali e cognitive dell’esperienza estetica»[19].
In una sua ricerca, pubblicata nel 2014, un gruppo di matematici doveva esprimere il proprio giudizio estetico rispetto a sessanta equazioni, mentre ne veniva registrata l’attività cerebrale per mezzo della risonanza magnetica funzionale (fMRI). I risultati dell’esperimento hanno mostrato, in particolare, l’attivazione di una specifica area nel cervello dei soggetti analizzati, una zona dove «c’è sempre attività neuronale quando si ha esperienza di bellezza»[20], a prescindere dalla sua fonte (un quadro, un brano musicale, un’equazione ecc.). La regione individuata è connessa alle emozioni e viene indicata come «campo A1 della corteccia orbito-frontale mediale (mOFC)»[21]; specifichiamo inoltre che «più la formula è considerata bella e più intensamente si attiva quest’area»[22].
I risultati dell’esperimento non sorprendono i matematici; per esempio, Colin Adams afferma: «“quando vedo una bellissima costruzione matematica, […], provo la stessa sensazione di quando osservo qualche forma di arte che mi colpisce”»[23]. Gli fa eco Daina Taimina, la quale ritiene che le belle soluzioni matematiche «“suonano come una melodia”»[24].
Infine, l’indagine condotta dal professor Zeki ha rivelato che non tutte le equazioni sono belle allo stesso modo: alcune risultano più attraenti di altre. Infatti, nonostante la soggettività che può intervenire in un qualunque giudizio estetico, i partecipanti alla ricerca hanno mostrato quasi unanimemente la propria preferenza per un’equazione in particolare, l’identità di Eulero[25]:
eiπ + 1 = 0
Secondo Adams, tale formula «“richiede complessivamente non più di sette simboli per essere scritta: è sbalorditivo”»[26]. Per i matematici essa rappresenta «una combinazione irresistibile, perché lega cinque costanti fondamentali con tre operazioni aritmetiche basilari»[27].
3. UN «ESTETA DELLA SCIENZA»[28]: PAUL DIRAC E IL “PRINCIPIO DI BELLEZZA MATEMATICA”
Paul Adrien Maurice Dirac (1902-1984) è uno dei più importanti fisici del Novecento. Nato a Bristol, Nobel per la Fisica nel 1933, tra i suoi numerosi contributi ricordiamo, per esempio, la «sintesi tra relatività speciale e meccanica quantistica»[29]; inoltre, la sua equazione[30]
(ið – m) ψ = 0
ha previsto l’esistenza di una nuova particella, il positrone[31], la cui scoperta empirica ha aperto il mondo dell’antimateria alla fisica contemporanea.
In questo articolo ci concentriamo su una delle sue “credenze fondamentali”, ovvero il «principio di bellezza matematica»[32], un concetto che, per Dirac, detiene «una duplice funzione: di guida euristica e di criterio valutativo»[33]. Cosa si intende con “bellezza matematica”? Lo stesso Dirac, in uno scritto del 1939, specifica che essa non si può spiegare con precisione ma aggiunge che, nel coglierla, «gli studiosi di matematica non hanno alcuna difficoltà»[34].
Convinto che i criteri estetici dirigano la ricerca scientifica, il fisico inglese non esita a difendere la bellezza delle equazioni anche in caso di contrasto con i dati empirici: «è più importante che le equazioni siano belle piuttosto che in accordo con gli esperimenti»[35].
Quando in fisica si deve elaborare una nuova teoria, Dirac sostiene che, prima di tutto, bisogna individuarne l’impalcatura matematica, ma questa scelta deve seguire una direzione precisa: «bisognerebbe lasciarsi guidare da considerazioni di bellezza matematica»[36]; in un testo successivo, scrive che «se si lavora con il proposito di ottenere equazioni dotate di bellezza, e si possiede un’intuizione davvero solida, si è sicuramente sulla strada del progresso»[37]. In caso di reiterato disaccordo tra ipotesi ed esperimenti, per Dirac si può modificare la teoria, purché se ne sviluppi una con struttura matematica di ancora maggior bellezza.
Dirac elogia la relatività di Einstein: secondo lui, la teoria einsteiniana «ha introdotto – in una misura che non ha precedenti – la bellezza matematica nella descrizione della Natura»[38]. Lo scienziato di Bristol sostiene come sia stata proprio la sua bellezza a permettere alla relatività di ottenere credito presso i fisici. Inoltre, Dirac afferma che Einstein «era guidato solo da considerazioni relative alla bellezza delle equazioni»[39], e che «tutto il suo modo di procedere tendeva alla ricerca di una teoria bella»[40].
In uno scritto del 1979, Dirac elenca alcuni esperimenti che hanno confermato la teoria di Einstein, ma a un certo punto si chiede come ci si debba muovere in caso di contrasto fra questa concezione scientifica e le sue verifiche empiriche. Egli rifiuta nettamente l’idea che la relatività possa essere errata, perché «chiunque apprezzi la fondamentale armonia che esiste tra il modo in cui funziona la Natura e alcuni princìpi matematici generali non può non sentire che una teoria di tale bellezza ed eleganza deve essere sostanzialmente corretta»[41], a prescindere dal fatto che essa sia in sintonia (o meno) con le osservazioni.
Dirac – secondo il fisico Freeman Dyson – «“ancor più di Newton e di Einstein, usò il criterio di bellezza come un modo per trovare la verità”»[42].
CONCLUSIONI
All’inizio del nostro percorso abbiamo usato l’immagine delle rette parallele per illustrare la concezione da decostruire, quella che considera scienza e bellezza come due argomenti disgiunti. Questo lavoro ha mostrato come, anziché conferire di rette parallele, si dovrebbe parlare invece di una vera e propria rete epistemologica per spiegare gli intrecci e i collegamenti che uniscono impresa scientifica e filosofia estetica.
Scienziati e scienziate sono esseri umani e anche loro hanno bisogno di quella cosa tanto familiare eppure così misteriosa, ovvia e sfuggente allo stesso tempo, che è la bellezza. Può sembrare una banalità, ma la visione odierna della scienza ha offuscato simili ragionamenti, col risultato di farci separare ambiti che si arricchiscono a vicenda, se li facciamo comunicare.
A questo punto della trattazione, al lettore o alla lettrice è forse rimasta in sospeso una domanda fondamentale: “dunque, che cos’è la bellezza matematica?”. Rispondiamo a tale quesito avvalendoci della legge di gravitazione universale di Newton:
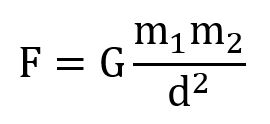 Dove:
Dove:
“F” designa la forza d’attrazione,
“G” è la costante di gravitazione universale[43],
“m” indica le masse dei due corpi che dobbiamo considerare,
“d” rappresenta la loro distanza (espressa al quadrato).
Questa formula mostra che la forza d’attrazione gravitazionale tra due corpi aumenta al crescere delle loro masse, mentre diminuisce all’aumentare della loro distanza. Semplice e logico, vero? Anche la chiarezza fa parte del fascino di questa legge fisica.
Perché tale equazione è così bella? Prima di tutto, si trova scritta in una forma compatta ed elegante, senza risultare eccessivamente contorta né dal punto di vista del significato, né tantomeno da quello del significante.
La sua ampia efficacia empirica rende questa formula particolarmente versatile, anche al giorno d’oggi. Essa serve a spiegare fenomeni fisici che valgono sia sul pianeta Terra sia nell’Universo, dal momento che unisce le leggi di Galileo (che riguardano i fenomeni terrestri) con quelle di Keplero (valevoli invece per il macrocosmo); inoltre, grazie a questa legge, «Newton è in grado di inquadrare e spiegare un’amplissima serie di fenomeni, […] riuscendo anche a risolvere una gran quantità di questioni fisiche e astronomiche rimaste fino ad allora senza una risposta adeguata»[44].
Studiare le equazioni matematiche nella loro storicità le rende meno enigmatiche, più attraenti e più “umane”, perché sono umani coloro che le hanno formulate nei secoli, con le loro idee e visioni del mondo.
A tal proposito, sarà curioso sapere che Newton si occupò anche di ambiti che attualmente non rientrano nella scienza ufficiale come, per esempio, l’alchimia; questi interessi possono aver influenzato il lavoro scientifico di questo autore. La sua legge di gravitazione universale è, in un certo senso, “magica”; infatti, tale equazione prevede che due corpi interagiscano senza che ci sia contatto diretto tra loro, un’idea inconcepibile per Cartesio o Leibniz e che Newton stesso faticava ad accettare, ma «la nascose dietro al formalismo matematico con la sua indubbia efficacia»[45]. Al giorno d’oggi, grazie al concetto di “campo”, questo fenomeno ci appare come qualcosa di assodato, ma all’epoca era un’intuizione rivoluzionaria.
Semplicità, chiarezza ed efficacia, insieme alle considerazioni espresse fin qui, concorrono a rendere affascinante un’equazione matematica, ne eliminano quell’impressione di freddo distacco e la trasformano in qualcosa di vivo e appassionante.
Chiediamoci ora: un quadro, un brano musicale, una statua o un’equazione sono davvero entità così diverse? Sono magnifiche espressioni che generano bellezza, un sentimento umano profondo e necessario, che influenza il nostro quotidiano, orienta le nostre scelte e, last but not least, ci fa stare bene.
NOTE
[1] Dyson, F. (1956). Obituary of Hermann Weyl. Nature 177, 457–458, citato in: Frontiers | The experience of mathematical beauty and its neural correlates (frontiersin.org)
[2] estetica nell'Enciclopedia Treccani - Treccani
[3] Ibidem.
[4] Ubaldo Nicola, Atlante illustrato di Filosofia, Firenze-Milano, Giunti Editore, 1999-2005, p. 566.
[5] Franco Bertini, Io penso, Bologna, Zanichelli editore, 20222, vol. I, p. 233.
[6] Ibidem.
[7] Platone, Fedro, in Tutte le opere, a cura di E. V. Maltese, premessa di G. Caccia, Roma, Newton Compton editori, 20102, p. 945.
[8] Franco Bertini, op. cit., p. 233.
[9] Riccardo Chiaradonna, Plotino, Roma, Carocci editore, 2009, p. 71. Corsivi dell’autore.
[10] Ibidem.
[11] Paolo D’Angelo et al., Estetica, a cura di E. Franzini e A. Somaini, Milano, Raffaello Cortina Editore, 2002, p. 71.
[12] Ibidem.
[13] Ivi, p. 11.
[14] Ivi, p. 125.
[15] Ibidem.
[16] Ibidem.
[17] Ivi, p. 126.
[18] Ivi, p. 125.
[19] Il senso della mente per la bellezza: intervista con Semir Zeki - Le Scienze
[20] Sesso, bellezza ed equazioni - Il Sole 24 ORE
[21] Ibidem.
[22] La bellezza delle formule matematiche | Lost in Galapagos (corriere.it)
[23] Il senso dei matematici per la bellezza delle equazioni - Le Scienze
[24] Ibidem.
[25] https://sciencecue.it/formula-matematica-identita-eulero/17295/
[26] Il senso dei matematici per la bellezza delle equazioni - Le Scienze
[27] La bellezza delle formule matematiche | Lost in Galapagos (corriere.it)
[28] La fisica tra verità e bellezza - Il Sole 24 ORE
[29] Ibidem.
[30] Questa è la versione corretta, seppur semplificata dell'equazione di Dirac, in cui la derivata parziale è "tagliata" (ð). In notazione più completa può essere scritta così: (iγμ∂μ - m) ψ = 0. La versione popolare (∂ + m) ψ = 0 è errata. Per approfondimenti: https://www.fe.infn.it/~bettoni/particelle/Lezione4-5.pdf
[31] Il positrone è l’antiparticella dell’elettrone; positroni ed elettroni hanno stessa massa e stesso spin, ma le rispettive cariche elettriche sono di segno opposto. Previsto teoricamente da Dirac nel 1928, il positrone è stato scoperto empiricamente da Anderson nel 1932.
[32] Paul A. M. Dirac, La bellezza come metodo, prefazione e a cura di V. Barone, Milano, Indiana Editore, 2013, p. 24.
[33] Ibidem.
[34] Ivi, p. 84
[35] Ivi, p. 104.
[36] Ivi, p. 87.
[37] Ivi, p. 104.
[38] Ivi, p. 84.
[39] Ivi, p. 175.
[40] Ibidem.
[41] Ivi, pp. 174-175. Corsivo dell’autore.
[42] È la matematica, bellezza! - Il Sole 24 ORE
[43] 6,67⋅10-11N⋅m2kg-2
[44] Newton in "Enciclopedia della Matematica" - Treccani
[45] Entanglement quantistico e viaggi nel tempo? - Controversie
BIBLIOGRAFIA
- Baker, J., 50 physics ideas you really need to know, London, Quercus Publishing, 2007, trad. it. 50 grandi idee di fisica, Bari, Edizioni Dedalo, 2009.
- Bertini, F., Io penso, Bologna, Zanichelli editore, 20222, 3 voll.
- Chiaradonna, R., Plotino, Roma, Carocci editore, 2009.
- D’Angelo, P., et al., Estetica, a cura di E. Franzini e A. Somaini, Milano, Raffaello Cortina Editore, 2002.
- Dirac, P.A.M., La bellezza come metodo, prefazione e a cura di Vincenzo Barone, Milano, Indiana Editore, 2013.
- Nicola, U., Atlante illustrato di Filosofia, Firenze-Milano, Giunti Editore, 1999-2005.
- Platone, Tutte le opere, a cura di E. V. Maltese, Roma, Newton Compton editori, 20102.
- Stewart, I., Seventeen Equations that Changed the World, London, Profile Books, 2012, trad. it. Le 17 equazioni che hanno cambiato il mondo, Torino, Giulio Einaudi editore, 2017-2018.
SITOGRAFIA
- Barone, V., La fisica tra verità e bellezza (La fisica tra verità e bellezza - Il Sole 24 ORE), Il Sole 24 Ore, 18 febbraio 2019.
- Bottazzini, U., È la matematica, bellezza! (È la matematica, bellezza! - Il Sole 24 ORE), Il Sole 24 Ore, 15 dicembre 2013.
- Bottazzini, U., La bellezza come “chiave” per la fisica (La bellezza come “chiave” per la fisica - Il Sole 24 ORE), Il Sole 24 Ore, 23 aprile 2019.
- Catania, A., CAMPO GRAVITAZIONALE (Campo gravitazionale (youmath.it)), YouMath, 2 maggio 2023.
- De Loa, J., Canone di bellezza nella storia: come è cambiato il concetto di bellezza dalla preistoria ad oggi (Canone di bellezza: come è cambiato l'ideale di bellezza dalla preistoria ad oggi | Studenti.it), Studenti.it.
- Leone, B., Isaac Newton e la gravitazione universale (Isaac Newton e la gravitazione universale | Studenti.it), Studenti.it, 29 dicembre 2009.
- Meldolesi, A., La bellezza delle formule matematiche (La bellezza delle formule matematiche | Lost in Galapagos (corriere.it)), Corriere della Sera, 16 febbraio 2014.
- Moskowitz, C., Equations Are Art inside a Mathematician’s Brain (Equations Are Art inside a Mathematician’s Brain - Scientific American), 4 marzo 2014, trad. it. Il senso dei matematici per la bellezza delle equazioni (Il senso dei matematici per la bellezza delle equazioni - Le Scienze), Le Scienze, 8 marzo 2014.
- Mussi, L., La legge della gravitazione universale di Isaac Newton (La legge della gravitazione universale di Isaac Newton (virgilio.it)), Virgilio Sapere.
- Panella, A., Entanglement quantistico e viaggi nel tempo? (Entanglement quantistico e viaggi nel tempo? - Controversie), Controversie, 31 ottobre 2023.
- Rosignolo, A., La bellezza tra filosofia, arte e moda (La bellezza tra filosofia, arte e moda - Aula di Lettere (zanichelli.it)), Zanichelli (Aula di Lettere), 24 novembre 2021.
- Sapere.it, La legge della gravitazione universale (La legge della gravitazione universale: La gravitazione universale - StudiaFacile | Sapere.it).
- Sgorbissa, F., Il senso della mente per la bellezza: intervista con Semir Zeki (Il senso della mente per la bellezza: intervista con Semir Zeki - Le Scienze), Le Scienze, 18 novembre 2022.
- Treccani, anagogia (anagogia in "Dizionario di filosofia" (treccani.it)), Dizionario di filosofia (2009).
- Treccani, campo (campo in "Enciclopedia dei ragazzi" - Treccani), Enciclopedia dei ragazzi (2005).
- Treccani, Dirac, Paul Adrien Maurice (Dirac, Paul Adrien Maurice nell'Enciclopedia Treccani), Enciclopedie on line.
- Treccani, ESTETICA (ESTETICA in "Enciclopedia Italiana" (treccani.it)), Enciclopedia Italiana - IX Appendice (2015).
- Treccani, estetica (estetica nell'Enciclopedia Treccani), Enciclopedie on line.
- Treccani, Filosofia e metodo scientifico da Bacone a Newton (Filosofia e metodo scientifico da Bacone a Newton in "Storia della civiltà europea a cura di Umberto Eco" - Treccani), Storia della civiltà europea a cura di Umberto Eco (2014).
- Treccani, L'Ottocento: fisica. L'elettromagnetismo e il campo (L'Ottocento: fisica. L'elettromagnetismo e il campo in "Storia della Scienza" - Treccani), Storia della Scienza (2003).
- Treccani, Newton (Newton in "Enciclopedia della Matematica" - Treccani), Enciclopedia della Matematica (2013).
- Treccani, Newton, Isaac (Newton, Isaac in "Dizionario di filosofia" - Treccani), Dizionario di filosofia (2009).
- Treccani, Newton, Isaac (Newton, Isaac in "Enciclopedia dei ragazzi" - Treccani), Enciclopedia dei ragazzi (2006).
- Treccani, particelle elementari (particelle elementari in "Enciclopedia dei ragazzi" (treccani.it)), Enciclopedia dei ragazzi (2006).
- Treccani, positrone (positrone in "Dizionario delle Scienze Fisiche" (treccani.it)), Dizionario delle Scienze Fisiche (1996).
- Treccani, scientismo (scientismo in "Dizionario di filosofia" (treccani.it)), Dizionario di filosofia (2009).
- Zeki, S., et al., The experience of mathematical beauty and its neural correlates (Frontiers | The experience of mathematical beauty and its neural correlates (frontiersin.org)), Frontiers in Human Neuroscience, 13 febbraio 2014.
- Zeki, S., Sesso, bellezza ed equazioni (Sesso, bellezza ed equazioni - Il Sole 24 ORE), trad. it., Il Sole 24 Ore, 21 aprile 2017.
Solaris, il racconto della scienza - Un manifesto
Noi uomini partiamo per il cosmo pronti a tutto:
alla solitudine, alla lotta, al martirio e alla morte.
Anche se per pudore non lo proclamiamo a gran voce,
spesso siamo convinti di essere persone straordinarie.
In realtà quello che vogliamo non è conquistare il cosmo,
ma estendere la Terra fino alle sue frontiere.[1]
PERCHÉ UNA RUBRICA CHIAMATA SOLARIS?
Solaris è un romanzo pubblicato da Stanislaw Lem nel 1961, l’anno in cui Jurij Alekseevič Gagarin accedeva allo spazio per la prima volta nella storia dell’umanità. È la storia di un incontro tra uno psicologo-astronauta e la forma di vita del pianeta Solaris. Ma è anche una riflessione sul senso del “contatto”, sulla straniante alterità del cosmo.
Solaris è un pianeta oceanico che non risponde all’umano: con apparente e incomprensibile volontà crea geometrie megalitiche e “quasi architettoniche”, materializza figure femminee estratte dall’inconscio di chi gli si avvicina e poi disfa ogni sua creazione nell’oblio della sua essenza marina.
“Perché il mondo parla?” Si chiede Kris Kelvin - lo psicologo coinvolto nello studio di Solaris e attorno a cui gira la narrazione - “vuole giocare con noi? O forse punirci?”[2]
----------
La letteratura parla della scienza esprimendone l’immagine sociale, la scienza parla infondendo le sue fantasie nelle storie che ci raccontiamo. Libri più o meno noti, pellicole apparentemente super partes partecipano collettivamente alla produzione degli immaginari scientifici e fantascientifici che finiscono inevitabilmente per influire sulle nostre aspettative future, sulla nostra percezione presente, sul modo in cui riorganizziamo il passato.
La letteratura, come le grandi cose, vive nel via vai che oscilla tra l’espressione e la descrizione.
Può raccontare la scienza che conosciamo, favorirne la diffusione; si pensi a Quando abbiamo smesso di capire il mondo (2021) di Benjamín Labatut o a La Bomba (2020) di Alcante, Bollet e Rodier.
La letteratura è avvertimento sul futuro e tentativo di previsione.
Günther Anders scriveva che autori come Huxley, Orwell o Lem lasciano indietro i filosofi che arrancano: i secondi indaffarati a definire chi ha fatto cosa, i primi preoccupati di cosa le cose faranno di noi.[3]
Tramite l’artificio e l’incanto si raccontano i timori di un’intera società, come nei grandi racconti socio-fantascientifici di James Graham Ballard o, ancora, nel romanzo scientifico-distopico che ha ispirato molti racconti del secolo scorso: Noi (1924) di Evgenij Ivanovič Zamjatin.
Alle volte la letteratura è la via privilegiata per testimoniare l’incontro del singolo - così piccolo - rispetto ai grandi Golem della scienza, della medicina, della tecnologia, del progresso.
Ne è esempio: Non morire di Anne Boyer, una lunga lettera di denuncia al mondo delle terapie contro il cancro che sarà oggetto di questa prima uscita.
D’altra parte, L’enorme bagaglio immaginativo di cui la letteratura si fa carico è ciò che, a sua volta, influenza inevitabilmente le pretese e le traiettorie di chi lavora attivamente nel mondo “scientifico”.
Ci sono le scienze, gli scienziati con il camice bianco, le tecnologie, le politiche di controllo e sviluppo, le controversie e le invidie, i dati e le persone.
Poi c’è Kris, “razionale e scientifico”, trascinato nell’alterità policroma di Solaris. C’è la solaristica, fatta di termini dotti ed esperti che su Solaris non avevano mai messo piede, pur scrivendone: solarista-ciberneti, solarista-simmetriologi… Infine c’è Lem che scrive una storia: sua, nostra? È sempre Kelvin a rispondere, rieccheggiando un noto aforisma di Proust: “non abbiamo bisogno di altri mondi, ma di specchi”.[4]
L’immenso insieme di queste storie mostra le scienze e le tecnologie nel rapporto che instaurano con la singola vita o con un gruppo sociale, con le speranze implicite di un’intera cultura, nel continuo gioco di scambi che le attraversa.
Perciò, noi che vi raccontiamo questi libri, non potevamo che chiamare Solaris questa rubrica: nell’amore per ciò che ci si racconta, speriamo che le parole possano parlarci ancora, e nuovamente.
NOTE
[1] S. Lem, Solaris (1961), a cura di M. Cataluccio, 2013, p. 108.
[2] S. Lem, Solaris, cit., p. 110.
[3] G. Anders, L'uomo è antiquato vol. II (1979), tr. it. M. A. Mori, Bollati Boringhieri editore, Torino 2007, p. 396.
[4] S. Lem, Solaris, cit., p. 109.
Matematica, filosofia e poetica della frattalità
Il matematico polacco Benoît Mandelbrot (1924-2010) diede per la prima volta nel 1975 una definizione della figura frattale: dall’aggettivo latino fractus, interrotto o irregolare, “frattale” designa un insieme di figure descrivibili dall’esterno ricorrendo a un insieme di proprietà geometrico-matematiche.
La figura frattale è internamente omotetica, le parti assomigliano al tutto. La sua dimensione non è necessariamente intera: un punto in geometria euclidea è di dimensione pari a 0, una linea pari a 1, una superficie pari a 2 e così via. La dimensione frattale può essere un numero frazionario, un numero irrazionale…
È frattale il cavolo romano, è frattale la curva di Koch (Fig. 1),[1] è frattale il gomitolo di lana, a “metà strada” tra la dimensione euclidea di una linea mono dimensionale (la corda di lana) e la dimensione euclidea di un volume (la sfera del gomitolo).[2]
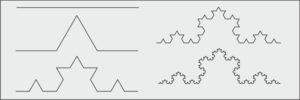
Fig.1
----------
Quando nasce il concetto di frattale?
Due acerrimi critici della sociologia della scienza come Alan Sokal e Jean Bricmont non hanno avuto dubbi: la frattalità fa parte del dominio delle matematiche. Di conseguenza, se le discipline umanistiche se ne sono appropriate ne hanno perpetrato un “reiterato abuso”.[3]
Teniamoci però a debita distanza: il padre dei frattali - al tempo - si definì “un vagabondo della scienza”.[4] Forse, il 1975 rappresenta una data troppo recente per poterci orientare. Mandelbrot rispose innanzitutto ad un’insufficienza della geometria, fino ad allora “troppo regolare e troppo fredda” per descrivere le insenature di una costa,[5] o i profili plastici e multiformi di una nuvola.[6]
Dove inizia questo vagabondaggio?
È il matematico polacco stesso a chiamare direttamente in causa un passato recondito.
In una lettera del 1695, Leibniz dichiarava a Bernoulli la possibilità di sviluppare una serie infinita mediante l’applicazione di un esponente frazionario a una base differenziale (d/dx)KF, così da “produrre una progressione geometrica, […] un’analogia meravigliosa”.[7]
Altrove, Leibniz fornisce una concezione teofanica e cosmologica della scalarità frattale: non solo è infinita la materia in perenne flusso in un mondo altrettanto infinito, ma sono infinite anche le anime e ciascuna “è uno specchio vivente perpetuo dell’universo”.[8] Ogni anima include l’intera serie del mondo che rispecchia dal proprio punto di vista, ogni punto di vista include oscuramente ogni altro. Sempre il filosofo tedesco, guardando per la prima volta nel microscopio progettato da Antonie van Leeuwenhoek (1632-1723) si meravigliò della qualità frattale degli organismi: “c’è un mondo di creature - di esseri viventi e di animali, di entelechie e di anime - anche nella più piccola porzione di materia”.[9]
Paolo Portoghesi (1931-2023) fu tra i primi a cogliere la profonda analogia tra le ricerche de Gli oggetti frattali e le architetture della sua amata Roma.[10]
A sua volta, Gilles Deleuze (1925-1995) ha avuto il merito di situare il Barocco a lato di Leibniz, in prossimità di Mandelbrot: l’architettura barocca si sviluppa passando “attraverso un numero infinito di punti angolosi, […] è la curva di Koch”.[11] Si pensi alle ipnotiche geometrie del Borromini (1599-1667) in Sant’Ivo alla Sapienza, alla cappella della Sacra Sindone del duomo di Torino progettata da padre Guarino Guarini (1624-1683) (Fig.2), all’utilizzo del bugnato con la sua qualità cavernosa.

Fig. 2
Possiamo andare ancora più in là, scorgere una qualità frattale nel radicale principio di pienezza di Giordano Bruno (1548-1600) o nei rapporti di autosimilarità astrologica che innervano le analogie micro e macro cosmiche dell’epoca rinascimentale.
Ancora, potremmo procedere a ritroso sino alle geometrie dell’architettura islamica,[12] come nei motivi decorativi dei “Muqarna” (مقرنص) (fig.3), oppure nel tempio di Brihadeshwara in India (fig.4).

Fig. 3
Fig. 4
Guardando alla storia dei giardini ritroviamo un doppia correlazione omotetica: è frattale la morfologia vegetale (le nervature delle foglie), ma qualcosa di frattale struttura le complesse razionalizzazioni arboree dell’orto botanico di Padova costruito nel 1545 (fig. 5),[13] oppure i giardini cinesi e giapponesi in cui la morfologia del paesaggio “in miniatura” dovrebbe rispecchiare il buon ordine del cosmo.[14]

Fig. 5
Cosa fare di tutta questa casistica? Imitazione della natura o sforzo descrittivo? Puro fatto artistico-espressivo? Cimeli di un passato incommensurabile?
Mandelbrot fu capace di sistematizzare sotto un unico nome un “museo degli orrori”[15]: la curva di Peano (fig.6) che passa per tutti i punti di un quadrato - paradosso di una superficie finita racchiusa da un perimetro infinito; la polvere di Cantor; le intuizioni di Jean Perrin che nel 1913 parlava di “curve senza tangente”.[16]
 Fig. 6
Fig. 6
Da allora la matematica frattale si è sviluppata in ogni direzione: nello studio delle fluttuazioni finanziare e nell’analisi dei dati biochimici, nella modellazione di fenomeni complessi e, non ultimo, nello sviluppo della Chaos theory a cui Henri Poincaré (1854-1912) diede un impulso fondamentale.
Dove collocare quel “reiterato abuso” dei concetti matematici a cui ci siamo precedentemente richiamati?
Si osservi ciò che scrivono Deleuze e Guattari in Mille piani (1980): l’interdimensionalità non è soltanto l’indicatore della dimensione non intera delle figure frattali, ma è anche segno di un divenire, di qualcosa che si muove tra i piani, una “zona di indiscernibilità propria del ‘divenire’”.[17] Un “tra” in cui la variazione prende vita: tutto ciò che è frattale sembra vivere e germogliare.
Parafrasando il matematico italiano Ernesto Cesaro (1859-1906), si potrebbe dire che la curva di Koch, se fosse viva, rinascerebbe in ogni punto dalle sue profondità.[18]
Le figure frattali hanno tuttavia un limite di scala, non vanno dall’infinitamente grande all’infinitamente piccolo: è una legge matematico-empirica che i due filosofi francesi sembrano violare apertamente.[19] È ciò che spinse Sokal e Bricmont ad affermare che la filosofia non aveva compreso il concetto.
Eppure, per un altro verso, Deleuze e Guattari ripropongono con un’espressione nuova le leggi imposte da Leibniz quasi tre secoli prima: l’anima è specchio dell’universo, ma si percepisce soltanto interamente come ininterrotta variazione metamorfica, rispecchiamento in perpetuo divenire dell’universo sin nelle sue più intime e infinite fibre.
É come l’esempio del movimento della mano proposto da Henri Bergson (1859-1941) ne L’evoluzione creatrice (1941): esternamente appare come figura (meccanicismo) o progetto (finalismo), ma a entrambe le visioni “manca l’essenziale: il divenire”.[20] Per Deleuze e Guattari è la rivendicazione di uno spazio dove al predominio della geometria euclidea si sostituisce l’imprevedibile variabilità della Natura, qualcosa di essenzialmente generativo. Pascal, navigando angosciosamente tra l’infinitamente grande e l’infinitamente piccolo, negava a sua volta le leggi imposte dalle vecchie corrispondenze simboliche micro e macro cosmiche a base di un solo infinito trascendente; Bruno contravveniva apertamente a una vecchia questio della scolastica secondo cui una creatura infinita era, per ciò stesso, contraddittoria.
----------
Dove arrestare questa violazione delle leggi determinate da ciascuna concettualizzazione?
C’è qualcosa di poetico, come scrive Franco Bifo Berardi: bisogna “far scivolare oltre il sistema stabilito dello scambio simbolico”.[21]
È proprio il filosofo italiano ad aver di recente risignificato la frattalità: segno sinistro - ma pur sempre segno - della frattalizzazione dei mercati e dello spazio pubblico (le bolle di cui si è tanto parlato non sono forse frattali?).
Riappare così l’ineliminabile figura di Leibniz: padre del contemporaneo panlogicismo metastabile e autovariante,[22] Berardi osserva che “gli individui sono frammenti di tempo precari, frattali uniformati dal processo di ricombinazione ininterrotta. […] il frattale automatizzato è il significato profondo dell’individualismo neoliberale”.[23]
Michel Serres (1930-2019), formatosi anch’egli su Leibniz, ha dato un nome a questo produttivo slittamento di principi, a questa non-regola dell’intromissione che sembra regnare anche nella storia della frattalità: parassitismo.[24]
Non dovrebbe sorprendere che anche il parassita sia frattale, è a un tempo parassitario e parassitato. Ed è sempre Michel Serres a chiedere: il parassita genera o corrompe il sistema?[25]
NOTE
[1] B. Mandelbrot, Gli oggetti frattali (1975), pp. 7-8. La curva di Kock è di dimensione=1,261859.
[2] B. Mandelbrot, The fractal geometry of nature, W. H. Freedman and company, San Francisco 1982, p. 404, p. 10.
[3] A. Sokal, J. Bricmont, Imposture intellettuali (1997), tr. it. F. Acerbi, M. Ugaglia, Garzanti, Milano 1999, p. 18.
[4] P. Portoghesi, Poesia della curva, Gangemi editore, Roma 2020, p. 61.
[5] B. Mandelbrot, Gli oggetti frattali, cit., pp. 21-44.
[6] B. Mandelbrot, The fractal geometry of nature, cit., p. 1.
[7] Ivi., p. 404.
[8] G. W. Leibniz, Monadologia (1720), tr. it. S. Cariati, Bompiani, Firenze 2017, p. 85, §56.
[9] Ivi, p. 89, §66.
[10] Si veda P. Portoghesi, Poesia della curva, cit., pp. 61-69.
[11] G. Deleuze, La piega (1988), tr. it. D. Tarizzo, Giulio Einaudi editore, Torino 1990, pp. 26-27. Per Irénée Scalbert anche l’arte gotica è contraddistinta da un principio di autosimilarità, si veda The nature of Gothic, AA Files, n. 72 (2016), pp. 73-77, 79-91, 93-95.
[12] P. Portoghesi, Poesia della curva, p. 62.
[13] Immagine tratta da L’invenzione del giardino occidentale, p. 56.
[14] Si veda P. Grimal, L’arte dei giardini (1974), Donzelli 2000, pp. 91-100.
[15] Mandelbrot, Gli oggetti frattali, cit., p. 01.
[16] Mandelbrot, 1977, The fractal geometry of nature, cit., p. 07.
[17] G. Deleuze, F. Guattari, Mille piani, p. 666. A p. 664,: “gli oggetti frattali” sono insiemi il cui numero di dimensioni è frazionario, non intero oppure intero, ma con variazione continua di direzione”. Mandelbrot scrive ne Gli oggetti frattali, p. 16, “là dove finora non si vedevano oche zone di transizione, […] io identifico delle zone frattali”.
[18] Si veda P. Portoghesi, Poesia della curva, cit., p. 64.
[19] Si veda B. Mandelbrot, The fractal geometry of nature, p. 783 e Gli oggetti frattali, pp. 21-44.
[20] H. Bergson, L’evoluzione creatrice, 1941, p. 81. Un esempio degno di nota è proposto da Tim Ingold in Siamo linee, p. 62, dove scrive che “il suolo, nella sua infinita varietà, ha una qualità frattale”.
[21] F. Bifo Berardi, Respirare, Luca Sossella editore, Roma 2019, p. 20.
[22] Ivi, p. 63.
[23] Ivi, p. 77.
[24] M. Serres, Il parassita (1980), a cura di G. Polizzi, Mimesis edizioni, Milano 2022.
[25] Ivi, p. 40.
BIBLIOGRAFIA
- Bergson, H., L’evoluzione creatrice (1941), tr. it. F. Polidori, Raffaello Cortina editore, Milano 2002.
- Bifo Berardi, F., Respirare, Luca Sossella editore, Roma 2019.
- Deleuze, G., Guattari, F., Mille piani (1980), tr. it. G. Passerone, Orthotes, Napoli-Salerno 2017.
- Deleuze, G., La piega (1988), tr. it. D. Tarizzo, Giulio Einaudi editore, Torino 1990
- Grimal, P., L’arte dei giardini (1974), tr. it. M. Magi, Donzelli editore, Roma, 2000.
- Ingold, T., Siamo linee (2015), it. D. Cavallini, Giovanni Treccani, Roma 2020
- Leibniz, G., W., Monadologia (1720), tr. it. S. Cariati, Bompiani, Firenze 2017.
- Mandelbrot, Benoît, “Is nature Fractal?”, Science, 1998, vol. 279, n. 5352, pp. 783-786.
- Mandelbrot, B., Gli oggetti frattali (1975), a cur di R. Pignoni, Giulio Einaudi editore, Torino 2000.
- Portoghesi, P., Poesia della curva, Gangemi editore, Roma 2020.
- Scalbert, I., The nature of Gothic, AA Files, n. 72 (2016), pp. 73-77, 79-91, 93-95.
- Serres, M., Il parassita (1980), a cura di G. Polizzi, Mimesis edizioni, Milano 2022.
- Sokal, , Bricmont, J., Imposture intellettuali (1997), tr. it. F. Acerbi, M. Ugaglia, Garzanti, Milano 1999.
- Vercelloni, M., Vercelloni, V., L’invenzione del giardino occidentale, Jaca Book, Firenze 2019.