Mai fidarsi della bellezza - Inganni e illusioni di un criterio scientifico
La bellezza può essere una splendida guida per lo sviluppo di formalismi matematici, ci suggerisce in questo blog Matteo Donolato (Che bella equazione! – Il ruolo della bellezza nelle scienze) seguendo il pensiero di P. Dirac.
Ai fisici teorici, in particolare, piace maneggiare teorie e oggetti matematici “belli”, addirittura considerano l’eleganza come un criterio di successo delle formulazioni teoriche, delle spiegazioni della realtà, delle descrizioni dei sistemi fisici.
Tuttavia sembra necessario essere cauti, perché a volte la bellezza matematica può nascondere dei tranelli.
Un bel formalismo matematico, infatti, ha il pregio di rendere la descrizione della realtà più semplice, più maneggevole, apparentemente più efficace e più elegante, ma, spesso, non rappresenta la realtà nel suo modo di essere effettivo, nei suoi comportamenti fenomenici.
Proviamo a fare qualche esempio:
- Il primo può essere l’identità di Eulero: è bellissima, compatta e semplice; comprende una serie di elementi che ricorrono in tutte le matematiche e geometrie – euclidee e non – ma, poiché è un’identità, non significa altro che un oggetto è identico a sé stesso, seppur descritto in modi diversi.
Esattamente come Hesperus e Vesperus, la stella del mattino e la stella della sera; nomi diversi per la stessa cosa, vista da angolazioni diverse, ma pur sempre una e una sola cosa è: il pianeta Venere.
L’identità di Eulero racconta di come la bellezza matematica possa diventare un formalismo di nessuna utilità nella pratica scientifica e applicativa.
È opportuno ricordare Husserl[1], quando accusava Galileo e, con lui, molta scienza della modernità, di realismo metafisico, di aver dimenticato – inseguendo i formalismi idealizzati – il contatto con il mondo delle cose reali.
Un secondo esempio – dobbiamo però per un attimo dimenticare che è stato falsificato nel ‘600 – è il modello geocentrico aristotelico-tolemaico dell’universo con la terra, con noi/io al centro di tutto. Cosa c’è di più bello, simmetrico, elegante, appagante, soprattutto per chi lo ha disegnato, di questo modello? Secondo il punto di vista antico era anche efficace nella rappresentazione della realtà. In parte anche per il nostro punto di vista: nella nostra esperienza quotidiana, non pare anche a noi di essere fermi, con il cielo che ci gira intorno?
Come sappiamo, però, questo schema non ha retto il confronto con i paradigmi successivi; per cui, è “caduto” ed è stato sostituito da un altrettanto elegante modello (quello di Newton) basato su un formalismo matematico, anch’esso, come ci dice Matteo Donolato, di grande bellezza: la legge della gravitazione universale.
Ecco, quindi, il terzo esempio: la legge di gravitazione universale si basa su un “oggetto scientifico”[2] misterioso e mai dimostrato: la forza di attrazione gravitazionale, cioè un’azione a distanza tra due corpi macroscopici.
“Oggetto” che è stato a sua volta sostituito, nella teoria della relatività, dalla nozione di campo gravitazionale. Che fa a meno della forza.
Il quarto ed ultimo esempio di bellezza teorica e matematica, nel campo della fisica delle particelle, è la Teoria supersimmetrica delle stringhe (o supersimmetria); questa teoria è in grado – grazie a dei formalismi matematici giudicati molto eleganti da quasi tutti i fisici – di descrivere il mondo dei bosoni e dei fermioni, e converge nella Teoria del Tutto: un tentativo di unificazione delle teorie quantistica e relativistica.
La “supersimmetria” – teoricamente – permetterebbe anche di aver a che fare con quantità e numeri vicine all’unità, che molti fisici definiscono “naturali”; e di evitare di far uso del cosiddetto “fine tuning”, cioè di aggiustamenti della teoria – assimilabili alle cinture di protezione di Lakatos – a fronte di casi particolari e risultati non allineati con le previsioni.
La teoria della supersimmetria, però, non sembra dare frutti sperimentali. Nessuno dei suoi risultati riesce a essere testato, con ovvio fastidio dei fisici che hanno puntato sulla sua produttività potenziale.
----------------
Al contrario, possiamo fare degli esempi di formalismi “non così belli” che – almeno per ora – sono di successo e (abbastanza) testati sperimentalmente.
Il modello che descrive una cosa apparentemente banale come i pennacchi di fumo (avete presente quelli che escono dalle ciminiere?) è costituito da un sistema di equazioni che - già in una approssimazione semplificata - riempiono almeno due pagine di un normale libro di testo – solo come formalismo matematico.
Purtroppo, un pennacchio di fumo non può essere descritto con formule prese dalla geometria solida; è, invece, un oggetto di grandissima complessità in cui compaiono più di un centinaio di fattori e termini e ancora non ne è descritta completamente la struttura. È più brutta di un orco delle favole. Ma funziona piuttosto bene.
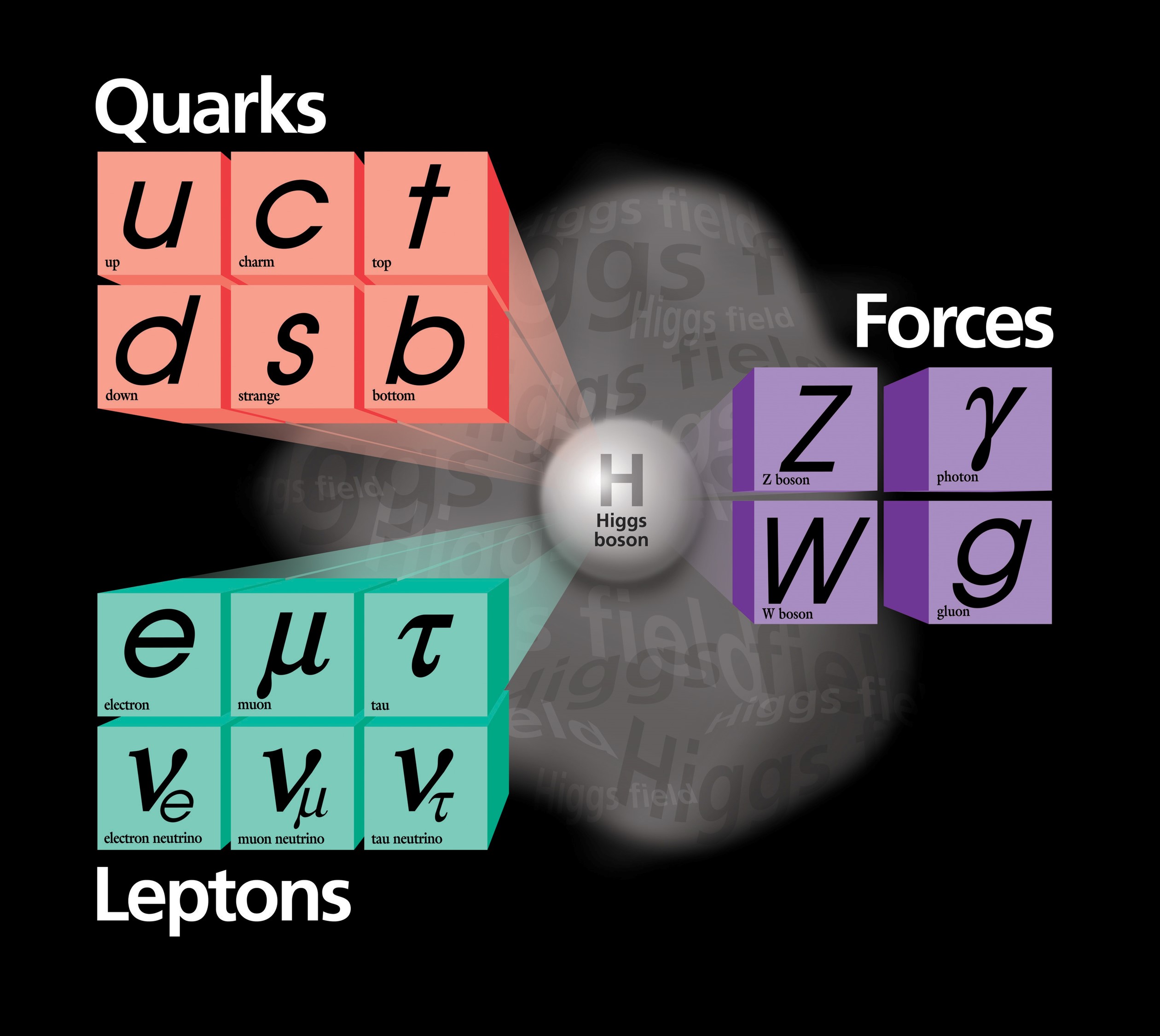
In fisica delle particelle, il "Modello standard", teoria che resiste da alcuni anni e che ha numerosi riscontri sperimentali – non ultima la rilevazione del bosone di Higgs, previsto anni prima e ora “trovato” e misurato sul campo – è abbastanza orribile, se misurata con il criterio della bellezza e dell’eleganza: più di 25 particelle “elementari”, tra cui: 6 fermioni detti quark; 8 gluoni privi di massa; 6 leptoni, che non partecipano alle interazioni forti; il fotone; 3 bosoni massivi; in ultimo il bosone di Higgs, massivo, neutro elettricamente e funzionale a dare massa a fermioni e bosoni. Tutti questi suddivisi in tre generazioni, in funzione della massa; inoltre, le generazioni non sono definite da criteri matematici a priori ma solo dalla necessità di “far funzionare” il modello (se mi si passa la semplificazione). “Vi delude che il modello standard sia così brutto?” dice Sabine Hossenfelder[3]
--------------
Sembra, quindi, estremamente pericoloso per i fisici, per i naturalisti - e direi persino per gli economisti - che desiderano descrivere in maniera realistica l’universo, affidarsi a dei formalismi molto belli.
Pericoloso perché il mondo e l’universo, nel loro presentarsi sono per lo più disuniformi, presentano continuamente singolarità, sfuggono al principio di omogeneità.
I casi eleganti come, ad esempio, le strutture polimorfe oggi chiamate frattali, sono eccezioni notevoli; tanto che uno strutturalista nato nella matematica come Roger Caillois, li presenta e li esalta proprio come eccezionalità, come fenomeni notevoli.
I salti, le catastrofi, le singolarità, sono la norma della realtà.
In fisica e nelle scienze naturali è meglio non fidarsi - e non affidarsi - alla bellezza matematica.
Si rischia di perdere la strada…
NOTE
[1] E. Husserl, La crisi delle scienze europee e la fenomenologia trascendentale, Il Saggiatore, Milano, 2015
[2] L. Daston, Biographies of scientific objects, The University of Chicago Press, Chicago and London, 2000
[3] S. Hossenfelder, Sedotti dalla matematica, Raffaello Cortina Editore, Milano, 2019, pag. 182
Che bella equazione! – Il ruolo della bellezza nelle scienze
«My work always tried to unite the true with the beautiful;
but when I had to choose one or the other,
I usually chose the beautiful»[1] (H. Weyl)
INTRODUZIONE
L’obiettivo di questo articolo è di riflettere sulla bellezza, una tematica apparentemente semplice e ordinaria ma che si rivelerà, nel corso dell’esposizione, un nucleo problematico da indagare attentamente.
Iniziamo la nostra disamina con una sezione filosofica, per sottolineare che siamo davanti a una questione complessa, che presenta sfumature concettuali profonde e antiche. Successivamente, analizzeremo questo tema da un punto di vista scientifico, con l’intento di mostrare come la bellezza entri a pieno diritto nei discorsi della scienza.
Lo scopo di questo scritto è di decostruire una narrazione ingenua, limitante e simil-scientista, che vede bellezza e scienza come due argomenti lontani e slegati, che non si incontrano mai, come due rette parallele. Mostreremo come tale separazione sia puramente convenzionale, contingente.
1. BELLEZZA E FILOSOFIA
In filosofia, l’analisi della bellezza ha origini antiche; questo tema viene indagato dall’estetica, una disciplina filosofica di ampio respiro che abbraccia numerose tesi e nuclei concettuali come, per esempio, «la produzione e i prodotti dell’arte»[2] o «il giudizio di gusto su di essi»[3].
Platone (427 ca.-347 ca. a.C.) sostiene che la bellezza è collegata all’ordine, alla proporzione e all’armonia; inoltre, la descrive come «la manifestazione più evidente del bene che permea tutte le cose»[4].
Nel Simposio, sviluppa l’idea secondo cui la bellezza attragga Eros (Amore), indicato come un “demone”, un’entità semidivina «sospesa fra cielo e terra»[5]; quindi, «l’amore viene stimolato dalla bellezza, […]: essa è il fine dell’amore, ciò verso cui l’amore riversa il suo slancio»[6].
Nel Fedro, inoltre, Platone afferma che la bellezza sensibile permette all’anima di ricordare l’idea di bellezza, perfetta e divina, ammirata prima dell’incarnazione. Pertanto, la bellezza del mondo fisico, nonostante sia molto lontana dalla compiutezza dell’idea, permette che lo spirito si elevi: «uno, al vedere la bellezza di quaggiù, ricordandosi della vera bellezza mette nuove ali»[7].
Per Platone esistono diverse tipologie di bellezza, ognuna delle quali occupa una posizione gerarchica distinta: sul gradino più basso incontriamo la bellezza del corpo mentre in cima troviamo la bellezza in sé, «idea eterna e immutabile di cui partecipano tutte le cose belle, sia fisiche sia spirituali»[8].
Plotino (205 ca.-270 ca. d.C.), figura centrale del neoplatonismo, «approfondisce e sviluppa la riflessione platonica sul bello, esposta nel Fedro e nel Simposio, associando il bello alla perfezione del mondo ideale»[9]; inoltre, questo autore dedica due trattati alla tematica della bellezza e la sua visione viene a volte qualificata come una “metafisica del bello”[10].
Nel testo enneadico Sul bello, in disaccordo con Platone, Plotino critica l’idea della bellezza considerata nei termini di armonia e proporzione delle parti, specificando che essa si trovi invece in qualità e oggetti semplici, poiché «ogni allontanamento dall’unità verso la molteplicità equivale a una perdita di perfezione»[11].
D’altra parte, Plotino condivide con Platone l’idea che la bellezza abbia valore anagogico, quando afferma che la bellezza sensibile è una tappa del percorso di purificazione dell’anima, cammino che la deve portare sempre più in alto nella scala dell’intelligibile: «compito dell’anima è […] di distogliere gradualmente la propria visione da quei corpi che non sono altro che “immagini e tracce e ombre” della vera fonte della bellezza, e, rientrando in sé, risalire verso quell’Uno […] circondato da ogni parte dal Bello, un “Bello che dispensa la bellezza a tutte le cose […]”»[12].
Pertanto, «è […] attraverso Plotino che si comprende come, nell’Antichità in generale, sia sempre più difficile, e spesso arbitrario, separare il problema della bellezza […] dalle costruzioni metafisiche in cui esso si inserisce»[13].
Infine, neanche per Edmund Burke (1729 ca.-1797) il bello può essere determinato secondo le categorie di armonia e proporzione, perché «l’ordine e la convenienza tra le parti sono […] qualità colte dall’intelletto, là dove l’effetto della bellezza è molto più immediato e sensibile»[14].
Burke contrappone la bellezza a un altro concetto, il sublime: la prima genera l’amore, «una passione […] sociale, intersoggettiva»[15], mentre il secondo dà origine al terrore, un’emozione collegata «alla tendenza di ogni individuo alla propria autopreservazione»[16]. Le divergenze, però, non terminano qui, in quanto il bello «nasce dalla visione di cose piccole e delicate, e dal contatto con tutto ciò che è liscio, levigato, sinuoso»[17]; al contrario, il sublime si origina, per esempio, dalla visione di spazi molto ampi (oceani, montagne ecc.) o dal «sentimento dell’infinito»[18].
2. SEMIR ZEKI E LA NEUROESTETICA: UNO STUDIO
Il neurobiologo Semir Zeki è ritenuto l’iniziatore della neuroestetica, «un filone di ricerca nell’ambito delle neuroscienze che indaga le basi neurali e cognitive dell’esperienza estetica»[19].
In una sua ricerca, pubblicata nel 2014, un gruppo di matematici doveva esprimere il proprio giudizio estetico rispetto a sessanta equazioni, mentre ne veniva registrata l’attività cerebrale per mezzo della risonanza magnetica funzionale (fMRI). I risultati dell’esperimento hanno mostrato, in particolare, l’attivazione di una specifica area nel cervello dei soggetti analizzati, una zona dove «c’è sempre attività neuronale quando si ha esperienza di bellezza»[20], a prescindere dalla sua fonte (un quadro, un brano musicale, un’equazione ecc.). La regione individuata è connessa alle emozioni e viene indicata come «campo A1 della corteccia orbito-frontale mediale (mOFC)»[21]; specifichiamo inoltre che «più la formula è considerata bella e più intensamente si attiva quest’area»[22].
I risultati dell’esperimento non sorprendono i matematici; per esempio, Colin Adams afferma: «“quando vedo una bellissima costruzione matematica, […], provo la stessa sensazione di quando osservo qualche forma di arte che mi colpisce”»[23]. Gli fa eco Daina Taimina, la quale ritiene che le belle soluzioni matematiche «“suonano come una melodia”»[24].
Infine, l’indagine condotta dal professor Zeki ha rivelato che non tutte le equazioni sono belle allo stesso modo: alcune risultano più attraenti di altre. Infatti, nonostante la soggettività che può intervenire in un qualunque giudizio estetico, i partecipanti alla ricerca hanno mostrato quasi unanimemente la propria preferenza per un’equazione in particolare, l’identità di Eulero[25]:
eiπ + 1 = 0
Secondo Adams, tale formula «“richiede complessivamente non più di sette simboli per essere scritta: è sbalorditivo”»[26]. Per i matematici essa rappresenta «una combinazione irresistibile, perché lega cinque costanti fondamentali con tre operazioni aritmetiche basilari»[27].
3. UN «ESTETA DELLA SCIENZA»[28]: PAUL DIRAC E IL “PRINCIPIO DI BELLEZZA MATEMATICA”
Paul Adrien Maurice Dirac (1902-1984) è uno dei più importanti fisici del Novecento. Nato a Bristol, Nobel per la Fisica nel 1933, tra i suoi numerosi contributi ricordiamo, per esempio, la «sintesi tra relatività speciale e meccanica quantistica»[29]; inoltre, la sua equazione[30]
(ið – m) ψ = 0
ha previsto l’esistenza di una nuova particella, il positrone[31], la cui scoperta empirica ha aperto il mondo dell’antimateria alla fisica contemporanea.
In questo articolo ci concentriamo su una delle sue “credenze fondamentali”, ovvero il «principio di bellezza matematica»[32], un concetto che, per Dirac, detiene «una duplice funzione: di guida euristica e di criterio valutativo»[33]. Cosa si intende con “bellezza matematica”? Lo stesso Dirac, in uno scritto del 1939, specifica che essa non si può spiegare con precisione ma aggiunge che, nel coglierla, «gli studiosi di matematica non hanno alcuna difficoltà»[34].
Convinto che i criteri estetici dirigano la ricerca scientifica, il fisico inglese non esita a difendere la bellezza delle equazioni anche in caso di contrasto con i dati empirici: «è più importante che le equazioni siano belle piuttosto che in accordo con gli esperimenti»[35].
Quando in fisica si deve elaborare una nuova teoria, Dirac sostiene che, prima di tutto, bisogna individuarne l’impalcatura matematica, ma questa scelta deve seguire una direzione precisa: «bisognerebbe lasciarsi guidare da considerazioni di bellezza matematica»[36]; in un testo successivo, scrive che «se si lavora con il proposito di ottenere equazioni dotate di bellezza, e si possiede un’intuizione davvero solida, si è sicuramente sulla strada del progresso»[37]. In caso di reiterato disaccordo tra ipotesi ed esperimenti, per Dirac si può modificare la teoria, purché se ne sviluppi una con struttura matematica di ancora maggior bellezza.
Dirac elogia la relatività di Einstein: secondo lui, la teoria einsteiniana «ha introdotto – in una misura che non ha precedenti – la bellezza matematica nella descrizione della Natura»[38]. Lo scienziato di Bristol sostiene come sia stata proprio la sua bellezza a permettere alla relatività di ottenere credito presso i fisici. Inoltre, Dirac afferma che Einstein «era guidato solo da considerazioni relative alla bellezza delle equazioni»[39], e che «tutto il suo modo di procedere tendeva alla ricerca di una teoria bella»[40].
In uno scritto del 1979, Dirac elenca alcuni esperimenti che hanno confermato la teoria di Einstein, ma a un certo punto si chiede come ci si debba muovere in caso di contrasto fra questa concezione scientifica e le sue verifiche empiriche. Egli rifiuta nettamente l’idea che la relatività possa essere errata, perché «chiunque apprezzi la fondamentale armonia che esiste tra il modo in cui funziona la Natura e alcuni princìpi matematici generali non può non sentire che una teoria di tale bellezza ed eleganza deve essere sostanzialmente corretta»[41], a prescindere dal fatto che essa sia in sintonia (o meno) con le osservazioni.
Dirac – secondo il fisico Freeman Dyson – «“ancor più di Newton e di Einstein, usò il criterio di bellezza come un modo per trovare la verità”»[42].
CONCLUSIONI
All’inizio del nostro percorso abbiamo usato l’immagine delle rette parallele per illustrare la concezione da decostruire, quella che considera scienza e bellezza come due argomenti disgiunti. Questo lavoro ha mostrato come, anziché conferire di rette parallele, si dovrebbe parlare invece di una vera e propria rete epistemologica per spiegare gli intrecci e i collegamenti che uniscono impresa scientifica e filosofia estetica.
Scienziati e scienziate sono esseri umani e anche loro hanno bisogno di quella cosa tanto familiare eppure così misteriosa, ovvia e sfuggente allo stesso tempo, che è la bellezza. Può sembrare una banalità, ma la visione odierna della scienza ha offuscato simili ragionamenti, col risultato di farci separare ambiti che si arricchiscono a vicenda, se li facciamo comunicare.
A questo punto della trattazione, al lettore o alla lettrice è forse rimasta in sospeso una domanda fondamentale: “dunque, che cos’è la bellezza matematica?”. Rispondiamo a tale quesito avvalendoci della legge di gravitazione universale di Newton:
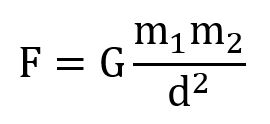 Dove:
Dove:
“F” designa la forza d’attrazione,
“G” è la costante di gravitazione universale[43],
“m” indica le masse dei due corpi che dobbiamo considerare,
“d” rappresenta la loro distanza (espressa al quadrato).
Questa formula mostra che la forza d’attrazione gravitazionale tra due corpi aumenta al crescere delle loro masse, mentre diminuisce all’aumentare della loro distanza. Semplice e logico, vero? Anche la chiarezza fa parte del fascino di questa legge fisica.
Perché tale equazione è così bella? Prima di tutto, si trova scritta in una forma compatta ed elegante, senza risultare eccessivamente contorta né dal punto di vista del significato, né tantomeno da quello del significante.
La sua ampia efficacia empirica rende questa formula particolarmente versatile, anche al giorno d’oggi. Essa serve a spiegare fenomeni fisici che valgono sia sul pianeta Terra sia nell’Universo, dal momento che unisce le leggi di Galileo (che riguardano i fenomeni terrestri) con quelle di Keplero (valevoli invece per il macrocosmo); inoltre, grazie a questa legge, «Newton è in grado di inquadrare e spiegare un’amplissima serie di fenomeni, […] riuscendo anche a risolvere una gran quantità di questioni fisiche e astronomiche rimaste fino ad allora senza una risposta adeguata»[44].
Studiare le equazioni matematiche nella loro storicità le rende meno enigmatiche, più attraenti e più “umane”, perché sono umani coloro che le hanno formulate nei secoli, con le loro idee e visioni del mondo.
A tal proposito, sarà curioso sapere che Newton si occupò anche di ambiti che attualmente non rientrano nella scienza ufficiale come, per esempio, l’alchimia; questi interessi possono aver influenzato il lavoro scientifico di questo autore. La sua legge di gravitazione universale è, in un certo senso, “magica”; infatti, tale equazione prevede che due corpi interagiscano senza che ci sia contatto diretto tra loro, un’idea inconcepibile per Cartesio o Leibniz e che Newton stesso faticava ad accettare, ma «la nascose dietro al formalismo matematico con la sua indubbia efficacia»[45]. Al giorno d’oggi, grazie al concetto di “campo”, questo fenomeno ci appare come qualcosa di assodato, ma all’epoca era un’intuizione rivoluzionaria.
Semplicità, chiarezza ed efficacia, insieme alle considerazioni espresse fin qui, concorrono a rendere affascinante un’equazione matematica, ne eliminano quell’impressione di freddo distacco e la trasformano in qualcosa di vivo e appassionante.
Chiediamoci ora: un quadro, un brano musicale, una statua o un’equazione sono davvero entità così diverse? Sono magnifiche espressioni che generano bellezza, un sentimento umano profondo e necessario, che influenza il nostro quotidiano, orienta le nostre scelte e, last but not least, ci fa stare bene.
NOTE
[1] Dyson, F. (1956). Obituary of Hermann Weyl. Nature 177, 457–458, citato in: Frontiers | The experience of mathematical beauty and its neural correlates (frontiersin.org)
[2] estetica nell'Enciclopedia Treccani - Treccani
[3] Ibidem.
[4] Ubaldo Nicola, Atlante illustrato di Filosofia, Firenze-Milano, Giunti Editore, 1999-2005, p. 566.
[5] Franco Bertini, Io penso, Bologna, Zanichelli editore, 20222, vol. I, p. 233.
[6] Ibidem.
[7] Platone, Fedro, in Tutte le opere, a cura di E. V. Maltese, premessa di G. Caccia, Roma, Newton Compton editori, 20102, p. 945.
[8] Franco Bertini, op. cit., p. 233.
[9] Riccardo Chiaradonna, Plotino, Roma, Carocci editore, 2009, p. 71. Corsivi dell’autore.
[10] Ibidem.
[11] Paolo D’Angelo et al., Estetica, a cura di E. Franzini e A. Somaini, Milano, Raffaello Cortina Editore, 2002, p. 71.
[12] Ibidem.
[13] Ivi, p. 11.
[14] Ivi, p. 125.
[15] Ibidem.
[16] Ibidem.
[17] Ivi, p. 126.
[18] Ivi, p. 125.
[19] Il senso della mente per la bellezza: intervista con Semir Zeki - Le Scienze
[20] Sesso, bellezza ed equazioni - Il Sole 24 ORE
[21] Ibidem.
[22] La bellezza delle formule matematiche | Lost in Galapagos (corriere.it)
[23] Il senso dei matematici per la bellezza delle equazioni - Le Scienze
[24] Ibidem.
[25] https://sciencecue.it/formula-matematica-identita-eulero/17295/
[26] Il senso dei matematici per la bellezza delle equazioni - Le Scienze
[27] La bellezza delle formule matematiche | Lost in Galapagos (corriere.it)
[28] La fisica tra verità e bellezza - Il Sole 24 ORE
[29] Ibidem.
[30] Questa è la versione corretta, seppur semplificata dell'equazione di Dirac, in cui la derivata parziale è "tagliata" (ð). In notazione più completa può essere scritta così: (iγμ∂μ - m) ψ = 0. La versione popolare (∂ + m) ψ = 0 è errata. Per approfondimenti: https://www.fe.infn.it/~bettoni/particelle/Lezione4-5.pdf
[31] Il positrone è l’antiparticella dell’elettrone; positroni ed elettroni hanno stessa massa e stesso spin, ma le rispettive cariche elettriche sono di segno opposto. Previsto teoricamente da Dirac nel 1928, il positrone è stato scoperto empiricamente da Anderson nel 1932.
[32] Paul A. M. Dirac, La bellezza come metodo, prefazione e a cura di V. Barone, Milano, Indiana Editore, 2013, p. 24.
[33] Ibidem.
[34] Ivi, p. 84
[35] Ivi, p. 104.
[36] Ivi, p. 87.
[37] Ivi, p. 104.
[38] Ivi, p. 84.
[39] Ivi, p. 175.
[40] Ibidem.
[41] Ivi, pp. 174-175. Corsivo dell’autore.
[42] È la matematica, bellezza! - Il Sole 24 ORE
[43] 6,67⋅10-11N⋅m2kg-2
[44] Newton in "Enciclopedia della Matematica" - Treccani
[45] Entanglement quantistico e viaggi nel tempo? - Controversie
BIBLIOGRAFIA
- Baker, J., 50 physics ideas you really need to know, London, Quercus Publishing, 2007, trad. it. 50 grandi idee di fisica, Bari, Edizioni Dedalo, 2009.
- Bertini, F., Io penso, Bologna, Zanichelli editore, 20222, 3 voll.
- Chiaradonna, R., Plotino, Roma, Carocci editore, 2009.
- D’Angelo, P., et al., Estetica, a cura di E. Franzini e A. Somaini, Milano, Raffaello Cortina Editore, 2002.
- Dirac, P.A.M., La bellezza come metodo, prefazione e a cura di Vincenzo Barone, Milano, Indiana Editore, 2013.
- Nicola, U., Atlante illustrato di Filosofia, Firenze-Milano, Giunti Editore, 1999-2005.
- Platone, Tutte le opere, a cura di E. V. Maltese, Roma, Newton Compton editori, 20102.
- Stewart, I., Seventeen Equations that Changed the World, London, Profile Books, 2012, trad. it. Le 17 equazioni che hanno cambiato il mondo, Torino, Giulio Einaudi editore, 2017-2018.
SITOGRAFIA
- Barone, V., La fisica tra verità e bellezza (La fisica tra verità e bellezza - Il Sole 24 ORE), Il Sole 24 Ore, 18 febbraio 2019.
- Bottazzini, U., È la matematica, bellezza! (È la matematica, bellezza! - Il Sole 24 ORE), Il Sole 24 Ore, 15 dicembre 2013.
- Bottazzini, U., La bellezza come “chiave” per la fisica (La bellezza come “chiave” per la fisica - Il Sole 24 ORE), Il Sole 24 Ore, 23 aprile 2019.
- Catania, A., CAMPO GRAVITAZIONALE (Campo gravitazionale (youmath.it)), YouMath, 2 maggio 2023.
- De Loa, J., Canone di bellezza nella storia: come è cambiato il concetto di bellezza dalla preistoria ad oggi (Canone di bellezza: come è cambiato l'ideale di bellezza dalla preistoria ad oggi | Studenti.it), Studenti.it.
- Leone, B., Isaac Newton e la gravitazione universale (Isaac Newton e la gravitazione universale | Studenti.it), Studenti.it, 29 dicembre 2009.
- Meldolesi, A., La bellezza delle formule matematiche (La bellezza delle formule matematiche | Lost in Galapagos (corriere.it)), Corriere della Sera, 16 febbraio 2014.
- Moskowitz, C., Equations Are Art inside a Mathematician’s Brain (Equations Are Art inside a Mathematician’s Brain - Scientific American), 4 marzo 2014, trad. it. Il senso dei matematici per la bellezza delle equazioni (Il senso dei matematici per la bellezza delle equazioni - Le Scienze), Le Scienze, 8 marzo 2014.
- Mussi, L., La legge della gravitazione universale di Isaac Newton (La legge della gravitazione universale di Isaac Newton (virgilio.it)), Virgilio Sapere.
- Panella, A., Entanglement quantistico e viaggi nel tempo? (Entanglement quantistico e viaggi nel tempo? - Controversie), Controversie, 31 ottobre 2023.
- Rosignolo, A., La bellezza tra filosofia, arte e moda (La bellezza tra filosofia, arte e moda - Aula di Lettere (zanichelli.it)), Zanichelli (Aula di Lettere), 24 novembre 2021.
- Sapere.it, La legge della gravitazione universale (La legge della gravitazione universale: La gravitazione universale - StudiaFacile | Sapere.it).
- Sgorbissa, F., Il senso della mente per la bellezza: intervista con Semir Zeki (Il senso della mente per la bellezza: intervista con Semir Zeki - Le Scienze), Le Scienze, 18 novembre 2022.
- Treccani, anagogia (anagogia in "Dizionario di filosofia" (treccani.it)), Dizionario di filosofia (2009).
- Treccani, campo (campo in "Enciclopedia dei ragazzi" - Treccani), Enciclopedia dei ragazzi (2005).
- Treccani, Dirac, Paul Adrien Maurice (Dirac, Paul Adrien Maurice nell'Enciclopedia Treccani), Enciclopedie on line.
- Treccani, ESTETICA (ESTETICA in "Enciclopedia Italiana" (treccani.it)), Enciclopedia Italiana - IX Appendice (2015).
- Treccani, estetica (estetica nell'Enciclopedia Treccani), Enciclopedie on line.
- Treccani, Filosofia e metodo scientifico da Bacone a Newton (Filosofia e metodo scientifico da Bacone a Newton in "Storia della civiltà europea a cura di Umberto Eco" - Treccani), Storia della civiltà europea a cura di Umberto Eco (2014).
- Treccani, L'Ottocento: fisica. L'elettromagnetismo e il campo (L'Ottocento: fisica. L'elettromagnetismo e il campo in "Storia della Scienza" - Treccani), Storia della Scienza (2003).
- Treccani, Newton (Newton in "Enciclopedia della Matematica" - Treccani), Enciclopedia della Matematica (2013).
- Treccani, Newton, Isaac (Newton, Isaac in "Dizionario di filosofia" - Treccani), Dizionario di filosofia (2009).
- Treccani, Newton, Isaac (Newton, Isaac in "Enciclopedia dei ragazzi" - Treccani), Enciclopedia dei ragazzi (2006).
- Treccani, particelle elementari (particelle elementari in "Enciclopedia dei ragazzi" (treccani.it)), Enciclopedia dei ragazzi (2006).
- Treccani, positrone (positrone in "Dizionario delle Scienze Fisiche" (treccani.it)), Dizionario delle Scienze Fisiche (1996).
- Treccani, scientismo (scientismo in "Dizionario di filosofia" (treccani.it)), Dizionario di filosofia (2009).
- Zeki, S., et al., The experience of mathematical beauty and its neural correlates (Frontiers | The experience of mathematical beauty and its neural correlates (frontiersin.org)), Frontiers in Human Neuroscience, 13 febbraio 2014.
- Zeki, S., Sesso, bellezza ed equazioni (Sesso, bellezza ed equazioni - Il Sole 24 ORE), trad. it., Il Sole 24 Ore, 21 aprile 2017.